
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нахождение комплексного показателя
|
|
Для определения значения х комплексного показателя Х, вначале производят оценку объекта исследования по всем частным показателям.
Пусть в нашем примере один объект исследования (институт) имеет такие показатели; 

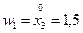 научных работ, где далее через
научных работ, где далее через  будем обозначать оценку каждого объекта исследования по
будем обозначать оценку каждого объекта исследования по
i -му показателю. Затем определяются значения функций принадлежностей по каждому терму для каждой лингвистической переменной:
 .
.
Полученные данные занесем в табл. 6.3.
Для каждого одинакового по содержанию (очень плохой результат; плохой; средний; хороший и очень хороший) терма получим взвешенную с коэффициентами приоритетности оценки:
 . (6.44)
. (6.44)
Для рассматриваемого примера, используя коэффициенты, полученные по методу Фишберна и данные табл. 6.3, получаем:
 ;
;
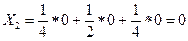 ;
;
 ;
;
 ;
;
 .
.
Эти данные также заносим в табл. 6.3 (нижняя строка).
Таблица 6.3
| Показатель | Термы | ||||
| Очень низкий | Низкий | Средний | Высокий | Очень высокий | |
| Y | m11(y 1) = 0 | m12(y 1) = 0 | m13(y 1) = 0 | m14(y 1) = 1 | m15(y 1) = 0 |
| Z | m21(z 1) = 0 | m22(z 1) = 0 | m23(z 1) = 0 | m24(z 1) = 0, 5 | m25(z 1) = 0, 5 |
| W | m31(w 1) = 0 | m32(w 1) = 0 | m33(w 1) = 0 | m34(w 1) = 1 | m35(w 1) = 0 |

| 0, 75 | 0, 25 |
Оценку обобщенного показателя качества находим по формуле:
 , (6.45)
, (6.45)
где 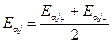 – середина a-среза нечёткого терма Еj
– середина a-среза нечёткого терма Еj
лингвистической переменной “КАЧЕСТВО”;
 – левая и правая границы множества
– левая и правая границы множества
a-уровня (a-среза нечёткого терма Еj).
При симметричных боковых ветвях функций принадлежности Е a j середина a-среза нечёткого терма Еj равна координате середины ядра Еj.
На практике часто берут a = 1. Для рассматриваемого примера при a = 1 получаем:
 ; E a2 = 0, 25; E a3 = 0, 45; E a4 = 0, 65; E a5 = 0, 9.
; E a2 = 0, 25; E a3 = 0, 45; E a4 = 0, 65; E a5 = 0, 9.
Тогда обобщенный показатель будет равен:

Как видно из рис. 6.21, при х = 0, 713 качество исследуемого объекта соответствует терму “Высокий результат” с функцией принадлежности (степенью достоверности) m4(0, 713) = 0, 7, и терму “Очень высокий результат” с функцией принадлежности (степенью достоверности) m5(0, 713) = 0, 13, а всем остальным термам с функцией принадлежности, равной нулю.
Таким образом, качество объекта, рассматриваемого в примере, более чем высокое.
По обобщенному показателю различные исследуемые объекты сравниваются между собой.
В случае, когда оценки по различным показателям задаются нечёткими величинами, функции принадлежности по каждому терму для каждой лингвистической переменной m ij могут определяться путем:
· дефазификации нечётких оценок;
· использования индексов ранжирования для сравнения нечётких переменных соответствующих термов и нечётких оценок по различным показателям.