Метод последовательных уступок

Метод последовательных уступок решения многокритериальных задач применяется в случае, когда частные критерии могут быть упорядочены в порядке убывающей важности, и заключается в следующем.

Пусть нумерация критериев соответствует их важности, т.е. f ₁(x) - наиболее важный критерий, f_n (x) - наименее важный.

На первом шаге решается задача оптимизации по критерию f ₁(x):

. (5.27)

Пусть f ₁^¢ - минимальное значение критерия в задаче (5.27). Далее назначается, исходя из практических соображений и принятой точности, некоторая уступка , которую субъект риска согласен допустить в f ₁(x). Тогда на втором шаге ищется решение, минимизирующее f ₂(x), при ограничении, что , т.е. решается задача

(5.28)

На k -м шаге решается задача

и т.д. до n -го шага. Этот метод, однако, может и не привести к эффективному решению.

В заключение отметим, что выбор критерия свертки частных критериев в задаче многокритериальной оптимизации чаще всего является не математической задачей и в каждой конкретной ситуации решается по-своему. Окончательное решение лучше принимать путем решения задач по различным обобщенным критериям, на основе анализа устойчивости и чувствительности к изменению критериев и исходных данных.

6. Принятие решений на основе нечёткой информации

Пойди туда – не знаю куда!

Принеси то – не знаю что!

Русская народная сказка

6.1. Неопределённость и неточность

Единичность реализации проектов, а следовательно, невозможность иметь презентабельную и однородную статистику для принятия решений вынуждает искать не стохастические методы представления неполноты информации, необходимой для прогнозирования исхода (результата) решения. Кроме того, сама природа неполноты (недостаточности) информации часто не является стохастической, что особенно присуще коммерческим проектам. Например, влияние макрополитических процессов на налоговое законодательство носит совершенно не стохастический характер, но недостаточная информативность в возможных изменениях налоговых законов может привести к краху коммерческого проекта.

Недостаточность (неполнота) информации у ЛПР имеет две стороны: неопределённость и неточность.

Степень неопределённости информации задаётся, например, с помощью квалификаторов “возможно”, “навер­няка”, “вероятно”, “может быть” и др.. Причём квалификатор “вероятно” может носить как стохастический характер, так и характер субъективного суждения (эпистомологический).

Неточность определяется границами (размерами) задания информационного множества. Примером неточного высказывания является “Данный проект даст доходность не менее 5%”. А такое высказывание: “Вероятно, что данный проект даст большую доходность”, содержит неопределённость, характеризующуюся словам – “вероятно” и неточность информации, словом – “большую”.

Очевидно, что между неопределённостью и неточностью существует противоречие, которое выражается в том, что с повышением точности информации возрастает ёё неопределённость. И, наоборот, уменьшение неопределённости приводит в общем случае к увеличению неточности информации.

Хотя в стохастических моделях объектов риска также имеется неопределённость и неточность, но эти модели требуют обработки точной, но распределённой по реализациям информации. Как только возникает неточность в оценке отдельных реализаций, стохастическая модель становится неприемлемой.

Наступивший век – век искусственного интеллекта и экспертных систем, в которых используются такие неопределённые и неточные понятия, как и в рассуждениях человека. Такие системы оперируют нечёткими понятиями, для описания которых создана теория нечётких множеств (fuzzy sets). Эта теория, основоположником которой является Лотфи Заде (Lotfi Zadeh), позволяет описывать неточную и неопределённую информацию с помощью нечётких множеств, а также оперировать этими множествами.

В настоящее время нечёткие системами принятия решений используются в промышленных роботах, в системах автоматического распознавания речи и изображений, в системах управления поездами метро и бытовыми приборами и других областях.

Нечёткое моделирование более естественно описывает характер человеческого мышления, чем традиционное формально-логическое моделирование, и позволяет получать лучшие результаты в системах управления с неполной информацией, что и обуславливает перспективность применения его в теории принятия управленческих решений [1, 3, 24].

6.2. Основные понятия теории нечётких множеств

Нечёткое множество (fuzzy set) представляет собой совокупность элементов произвольной природы, относительно которых нельзя с полной определённостью утверждать – принадлежит ли тот или иной элемент рассматриваемой совокупности данному множеству или нет.

Математически нечёткое множество определяется как множество упорядоченных пар или кортежа (последовательности элементов) вида:

,

где х – элемент некоторого универсального множества (универсума) – полного множества, охватывающего всю проблемную область) Х;

m _А (х) – функция принадлежности, которая ставит в соответствие каждому из элементов х Î Х некоторое число из интервала [0; 1].

При этом, если m _А (х ₀) = 1, то это означает, что элемент х ₀ достоверно принадлежит нечёткому множеству А, а если m _А (х ₀) = 0, то определённо не принадлежит. Чем в большей степени элемент х принадлежит нечёткому множеству А, тем ближе значение функции принадлежности m _А (х) к единице. И наоборот, чем в меньшей степени х принадлежит нечёткому множеству А, тем ближе значение функции принадлежности m _А (х) к нулю.

Пример. Множество Х, описывающее для ЛПР проблемную область, состоит из следующих элементов: х ₁ – автомобиль “Таврия”; х ₂ – “Жигули”; х ₃ – “Волга”, х ₄ – “ДЭУ”. Тогда нечёткое множество А “хороший автомобиль” может быть представлено следующим образом:

.

Это нечёткое множество надо понимать так: автомобиль “Жигули” относится к “хорошему автомобилю” с абсолютной достоверностью (m _А (х ₂) = 1), а вот автомобиль “Таврия” относится к нечёткому множеству А с малой степенью достоверности (m _А (х ₁) = 0, 3) и т.д.

Другая используемая запись конечного нечёткого множества (НМ) имеет вид

или

,

где п – число элементов НМ.

В случае непрерывного НМ функция принадлежности задаётся либо аналитическим выражением, либо графически (рис.6.1.).

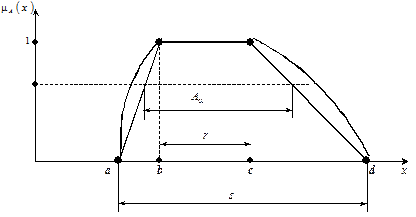
Рис. 6.1. Функции принадлежности непрерывного НМ

Формально определение НМ не накладывает никаких ограничений на выбор вида функций принадлежности (её боковые ветви могут быть экспоненциальными, гауссовыми, синусоидальными, линейными и др.).

Однако на практике наиболее широко используется трапециевидный вид функций принадлежности, что значительно упрощает математические операции с НМ, и практически не снижает общности полученных результатов [15].

В этом случае нечёткое множество полностью определяется только четырьмя элементами (а, b, c, d). Левая ветвь функции принадлежности имеет аналитический вид:

, (6.1)

а правая ветвь:

. (6.2)

Отметим, что небольшая ошибка в определении границ НМ (чисел а, b, c, d) является менее значимой, чем при представлении данного множества интервалом. При необходимости на этапе коррекции нечёткой модели вид функции принадлежности НМ (значения а, b, c, d) может быть уточнен.

Носителем s нечёткого множества А называется множество, которое содержит только те элементы универсального множества, для которых значения функции принадлежности отличны от нуля:

Ядром r нечёткого множества A называется множество, которое содержит только те элементы универсального множества, для которых функция принадлежности m _А (х) = 1:

.

Множеством a-уровня или a-срезом A _ нечёткого множества A называется множество, для элементов которого m _А (х) ³ a, где a – некоторое действительное число из интервала [0; 1]:

.

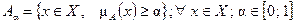Очевидно, что носитель s = A ₀ а ядро r = A ₁.

Для приведенного выше конечного нечёткого множества В и a = 0, 6 множество a уровня имеет вид В _a = (х ₂; х ₃; х ₄). Для непрерывного нечёткого множества a-срез А _a показан на рис.6.1.

Нечёткое множество называется нормальным, если максимальное значение его функции принадлежности равно единице, а если это условие не выполняется то – субнормальным. Субнормальное нечёткое множество приводят к нормальному (нормализуют) путём деления его функции принадлежности на её максимальное значение:

. (6.3)

Нечёткой величиной называется произвольное нечёткое множество, заданное на множестве действительных чисел R. Частным случаем нечёткой величины является нечёткое число.

Нечётким интервалом называется нечёткая величина с выпуклой и нормальной функцией принадлежности.

Нечётким числом A называется нечёткое множество, определённое на множестве действительных чисел R и имеющее нормальную выпуклую и унимодальную функцию принадлежности, т.е. и если , то .

Нечёткий нуль – это нечёткое число с модальным значением, равным нулю (рис.6.2).

Положительным (отрицательным) нечётким числом является то нечёткое число, у которого носитель является строго положительным (отрицательным).

Рис. 6.2. Вариант функции принадлежности нечёткого нуля

Нечёткой переменой называется кортеж á П, Х, А ñ, где
П – наименование нечёткой переменной; Х – область её определения; А = á х Î Х, m _А (х)Î [0; 1]ñ – нечёткое множество на Х, описывающее возможные значения, которые может принимать нечёткая переменная.

Пример. Нечёткая переменная “Актив с небольшой прибылью” может быть определён кортежем á П =Актив с небольшой прибылью; X Î (0; 20): A ñ, где А – нечёткое число с трапециевидной функцией принадлежности: A = (0; 0; 5; 20) (рис.6.3).

Рис. 6.3. Функция принадлежности нечёткой переменной “Актив с небольшой прибылью”

Лингвистической переменной называется кортеж
á П, T, O, X, G, M ñ, где П – наименование лингвистической переменной; Т – базовое терм множество лингвистической переменной (множество её значений (термов)), каждое из которых представляет нечёткую переменную, осмысленную в рассматриваемом контексте значений для данной лингвистической переменной); X – область определения (универсум) нечётких переменных, которые входят в определение лингвистической переменной П; G – некоторая синтаксическая процедура, описывающая процесс образования из множества Т новых, осмысленных в рассматриваемом контексте, значений для данной лингвистической переменной; M – семантическая процедура, позволяющая преобразовать каждое новое значение лингвистической переменной, образуемое процедурой G, в новую нечёткую переменную.

Пример. Лингвистическая переменная, которая оценивает эффективность принятого решения, может быть задана следующим кортежем: á Эффективность решения; , где термы Т = { T ₁ – низкая эффективность; T ₂ – средняя эффективность; T ₃ – высокая эффективность}. Обобщённый показатель эффективности Х принимает значение из интервала [0; 1]. G – может включать в себя новое значение “Невысокая эффективность”.

Семантическая процедура задания новых нечётких переменных будет рассмотрена ниже. Функции принадлежности термов показаны на рис.6.4.

Хотя функция принадлежности (m _А (х)) и характеризует возможность (но не вероятность) того, что значение х принадлежит нечёткому множеству А, на неё, в отличие от дискретной случайной величины или непрерывной случайной величины, на вероятности р_i или на плотность распределения вероятностей f (х) которых соответственно накладываются ограничения вида:

; и ,

накладывается лишь то ограничение, что она может принимать значения от нуля до единицы.

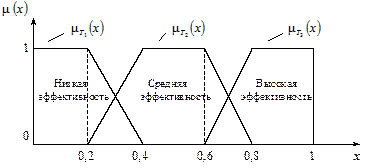
Рис. 6.4. Лингвистическая переменная “Эффективность решения”, состоящая из трёх термов

Одним из вопросов, возникающих при использовании теории нечётких множеств, является вопрос: “Как найти функции принадлежности этих множеств? ”