
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача классификации. Кластерный анализ .
|
|
Кластерный анализ - метод многомерного статистического анализа для решения задачи классификации данных. Задача классификации данных - выявления соответствующей структуры в них. Результат решения - разбиение множества исследуемых объектов и признаков на однородные в некотором понимании группы, или кластеры
Предполагается что, 1)выбранные характеристики допускают в принципе желательное разбиение на кластеры; 2)единицы измерения (масштаб) выбраны правильно.
Данные нормируют вычитанием среднего и делением на среднеквадратичное отклонение, так что дисперсия становится равной единицы, а математическое ожидание - нулю 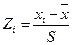
3)объекты представляются как множество точек в многомерном евклидовом пространстве; 4)каждый объект принадлежит одному и только одному подмножеству разбиения; 5) Происходит объединение объектов, схожих по всей совокупности факторов, и замена их некоторым усредненным объектом, что исключает дублирование данных; 6)объекты, принадлежащие одному и тому же кластеру - сходны, в то время, как объекты, принадлежащие разным кластерам - разнородны
Меры однородности объектов: 1. Евклидово расстояние
2. Линейное расстояние (хеммингово)
3. Sup-норма (расстояние Чебышева)
4.Обобщенное степенное растояние Минковского
5. Расстояние Махаланобиса
6. Манхетеннское («расстояние городских кварталов»)
7.обобщенное расстояние Колмогорова (Power distance)
Стратегии объединения кластеров:
1.Стратегия ближайшего соседа
2.Стратегия дальнего соседа (метод «полных связей»)
3.Стратегия группового среднего (метод «средней связи»)
4.Центроидная стратегия («центроидный метод»);
5. Стратегия, основанная на приращении суммы квадратов
Решением задачи кластерного анализа являются разбиения, удовлетворяющие некоторому критерию оптимальности. Этот критерий может представлять собой некоторый функционал, выражающий уровни желательности различных разбиений и группировок, который называют целевой функцией.
Критерии построения разбиения:
1) минимизация внутриклассовой инерции. Расстояние между классами определяется как разность моментов инерции двух последовательных разбиений, одно из которых получено из другого объединением рассматриваемых классов
2) минимизация полной инерции при объединении двух классов. Расстояние между классами определяется как момент инерции их объединения
3) минимизация дисперсии объединения двух классов. Расстояние между классами - дисперсия объединенного класса
Достоинства:
1)позволяет производить разбиение объектов не по одному параметру, а по целому набору признаков;
2)не накладывает никаких ограничений на вид рассматриваемых объектов, позволяет рассматривать множество исходных данных практически произвольной природы;
3)позволяет рассматривать достаточно большой объем информации и резко сокращать, сжимать большие массивы информации, делать их компактными и наглядными.
Недостатки и ограничения:
1)состав и количество кластеров зависит от выбираемых критериев разбиения;
2)при сведении исходного массива данных к более компактному виду могут возникать определенные искажения, а также могут теряться индивидуальные черты отдельных объектов за счет замены их характеристиками обобщенных значений параметров кластера
Описание алгоритма FOREL.
1. Все данные, которые нужно обработать, представляются в виде точек. Каждой точке соответствует вектор, имеющий n -координат. В координатах записываются значения параметров, соответствующих этим точкам.
2. Затем строится гиперсфера радиуса R1=Rmax, которая охватывает все точки. Если бы нам был нужен один таксон, то он был бы представлен именно этой начальной сферой.
3. Уменьшаем радиус на заранее заданную величину DR, т.е. R2=R1 - DR. Помещаем центр сферы в любую из имеющихся точек и запоминаем эту точку. Находим точки, расстояние до которых меньше радиуса, и вычисляем координаты центра тяжести этих " внутренних" точек. Переносим центр сферы в этот центр тяжести и снова находим внутренние точки. Сфера как бы «плывет» в сторону локального сгущения точек.
Такая процедура определения внутренних точек и переноса центра сферы продолжается до тех пор, пока сфера не остановится, т.е. пока на очередном шаге мы не обнаружим, что состав внут-ренних точек, а, следовательно, и их центр тяжести, не меняются. Это значит, что сфера остановилась в области локального максимума плотности точек в признаковом пространстве.
4. Точки, оказавшиеся внутри остановив-шейся сферы, мы объявляем принадлежа-щими кластеру номер 1 и исключаем их из даль-нейшего рассмотрения. Для оставшихся точек описанная выше процедура повторяется до тех пор, пока все точки не окажутся включенными в таксоны.
5. Каждый кластер характеризуется своим центром. Координаты центра кластера в данном случае вычисляются как средние арифметические соответствующих координат всех точек, попавших в данный кластер.
Здесь появляется параметр DR, определяемый исследователем чаще всего подбором в поисках компромисса: увеличение DR ведёт к росту скорости сходимости вычислительной процедуры, но при этом возрастает риск потери тонкостей таксономической структуры множества точек (объектов). Естественно ожидать, что с уменьшением радиуса гиперсфер количество выделенных таксонов будет увеличиваться.
27. Задача классификации. Дискриминантный анализ
Цель дискриминантного анализа – получение правил для классификации многомерных наблюдений в одну из нескольких категорий или совокупностей. Число классов известно заранее.
Дискриминация в две известные совокупности.
Рассмотрим задачу классификации одного многомерного наблюдения х = (х1, х2, …хр)/в одну из двух совокупностей. Для этих совокупностей известны р-мерные функции плотностей  т.е. известны как форма плотности, так и ее параметры. Напомним, что если в одномерном случае параметры нормального распределения задаются двумя скалярными величинами (мат. ожиданием и дисперсией), то в многомерном случае первым параметром служит вектор мат. ожиданий, а вторым – ковариационная матрица.
т.е. известны как форма плотности, так и ее параметры. Напомним, что если в одномерном случае параметры нормального распределения задаются двумя скалярными величинами (мат. ожиданием и дисперсией), то в многомерном случае первым параметром служит вектор мат. ожиданий, а вторым – ковариационная матрица.
Предположим, что р(1) и р(2) = 1-р(1) априорные вероятности появления наблюдения х из совокупностей 1 и 2. Тогда по теореме Байеса апостериорная вероятность того, что наблюдение х принадлежит совокупности 1  а апостериорная вероятность для х принадлежать совокупности 2
а апостериорная вероятность для х принадлежать совокупности 2 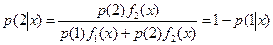
Классификация может быть осуществлена с помощью отношения 
Объект относим к классу 1, если это отношение больше 1, т.е. р(1 ׀ х)> 1/2, и ко второму классу, если это отношение меньше 1. Такая процедура минимизирует вероятность ошибочной классификации. При введении функции штрафа (потерь): с(2 ׀ 1) – цена ошибочной классификации наблюдения из совокупности 1 в класс 2, а с(1 ׀ 2) -
цена ошибочной классификации наблюдения из 2 в класс 1, решающее правило принимает вид 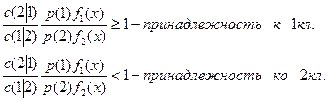
Итак, суть дискриминантного анализа состоит в следующем. Пусть известно о существовании двух или более генеральных совокупностей и даны выборки из каждой совокупности. Задача заключается в выработке основанного на имеющихся выборках правила, позволяющего приписать некоторый новый элемент к правильной генеральной совокупности, когда нам заведомо неизвестно о его принадлежности.
Суть дискриминантного анализа – разбиение выборочного пространства на непересекающиеся области. Разделение происходит с помощью дискриминантных функций. Число дискриминантных функций равно числу совокупностей. Элемент (новый) приписывается той совокупности, для которой соответствующая дискриминантная функция при подстановке выборочных значений имеет максимальное значение.
Алгоритм счёта:
1.среднее арифметическое переменных 
2.определяем сумму произведений отклонений от среднего значения 
3. ковариационная матрица состоит из элементов, которые вычисляются по следующей формуле
 где К – число групп. Т.е. для каждой группы строится ковариационная матрица, а потом объединенная. Размер 4х4. Складываем S12 для всех трех групп и делим на ∑ nk– K=15-3
где К – число групп. Т.е. для каждой группы строится ковариационная матрица, а потом объединенная. Размер 4х4. Складываем S12 для всех трех групп и делим на ∑ nk– K=15-3
4. Вычисляем обратную к объединенной ковариационной матрице (метод Жордана-Гаусса)
5. Вычисляем общие средние для всех переменных  j=1, M k=1, k;
j=1, M k=1, k;  - среднее j–й переменной в каждой к-й группе. Например
- среднее j–й переменной в каждой к-й группе. Например 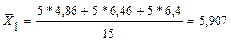
6. Вычисляем обобщенную D2статистику (расстояние Махалонобиса) 