Факторный анализ

Основная цель факторного анализа – обнаружить скрытые общие факторы, объясняющие связи между наблюдаемыми признаками. Исходные показатели для проведения факторного анализа также центрируются.

x₁, x₂ …x_p – исходные наблюдаемые показатели; y₁, y₂ …y_p’ – общие факторы, p’< p. x₁-m₁ = , j = 1…p.

q_jn - нагрузка общего фактора y_n на исходный показатель, u_j – остаточная случайная компонента, невязка. M[Y] = 0, M[U] = 0, D[Y] = 1; y и u попарно некоррелированны (r(y_i, y_j) =0, r(u_i, u_j) =0).

F – возможная с учетом ограничений линейная комбинация.

I_p’(Z(X))=1- , R_x –корреляционная матрица исходных данных, - корреляционная матрица = , - евклидова норма.

Найденные факторы y могут считаться причинами, а признаки x – следствиями.

30. Метод главных компонент

Задача заключается в определении такого набора 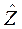, найденного на классе F допустимых преобразований исходных показателей x₁, x₂ …x_p, что .

F – всевозможные линейные ортогональные нормированные комбинации исходных показателей: Z_j(X) = c_j1(x₁-m₁)+…+ c_jp(x_p-m_p). 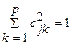; , i ¹ j. . В матричной форме = LX, – вектор искомых вспомогательных переменных, - матрица, строки которой удовлетворяют условиям ортогональности. 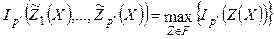. Переменные, полученные таким образом называются главными компонентами исследуемой системы показателей X. Первой главной компонентой ₁ (X) называется такая нормировано-центрированная линейная комбинация показателей, которая среди всех прочих линейных комбинаций имеет наибольшую дисперсию. , l ₁ – первая строка матрицы L.

Пусть X центрирована: X=X - 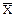, M[X] = 0, S = M[X X’] – ковариационная матрица.

l₁: (S-lI) 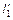=0 или det(S-lI)=0 – характеристическое уравнение матрицы S. Так как S - симметрична и неотрицательна, уравнение имеет p вещественных неотрицательных корней l₁³ …³ l₁ ³ 0.

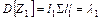, l₁ - наибольшее собственное значение. Первая главная компонента Z₁(X) = l₁X, l₁ – соответствующий l₁ собственный вектор.

Основные числовые характеристики главных компонент: M[Z]= M[L X]=L M[X] = 0; S_Z = M[Z Z’] = M[(L X) (L X)’]= M[LXX’ L’]= LM[XX’] L’=LSL’ – диагональная матрица, по диагонали стоят собственные числа.; D[Z_k]= l_k, k=1…p.

Кроме того, сумма дисперсий исходных признаков равняется сумме дисперсий главных компонент, а обобщенная дисперсия исходных признаков |S| равняется обобщенной дисперсии главных компонент |S_Z|.

Критерий информативности: , отсюда также можно получить ответ сколько (p’) главных компонент достаточно для качественного представления.

Использование главных компонент эффективно, когда все показатели X имеют одинаковую физическую природу (измеряются в одинаковых единицах). Иначе результаты исследования будут зависеть от выбора масштаба и природы единиц измерения.