
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение устойчивости, устойчивость по Ляпунову
|
|
Под устойчивостью функционирования сложной системы понимают способность системы сохранять требуемые свойства в условиях действий возмущений.
Рассматривая нелинейные системы вводят понятие устойчивости «в малом», «в большом», «в целом».
Система устойчива «в малом», если констатируют лишь факт наличия области устойчивости, но не определяют каким-либо образом ее границы. Систему называют устойчивой «в большом», когда определены границы области устойчивости, т.е. определены границы области начальных отклонений, при которых система возвращается в исходное состояние.
Когда система возвращается в исходное состояние при любых начальных условиях, систему называют устойчивой «в целом». Устойчивость «в целом» для определенного класса нелинейностей называют «абсолютной устойчивостью».
Постановка задачи. 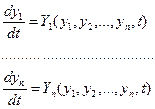 (1)
(1)
 y1…yn- вещественные переменные, характеризующие состояние системы.
y1…yn- вещественные переменные, характеризующие состояние системы.
Y1…Yn– известные функции, удовлетворяющие условию существования и единственности решения.
Невозмущенное движение – некоторое вполне определенное движение системы, подлежащее исследованию на устойчивость. Возмущению подвергаются только начальные условия.
Невозмущенному движению системы отвечает определенное частное решение ДУ (1) 
Дадим начальным значениям некоторое приращение ε

Движение системы, отвечающие измененным начальным условиям (4), есть возмущенное движение, а ε 1… ε n - возмущения.
Обозначим
yj – возмущенное движение fj - невозмущенное движение xj - отклонение или вариация xj=yj(t) – fj(t) (j =1…n) (5)
Если х1=0, …, хn=0 (6), то возмущенное движение совпадает с невозмущенным
Геометрически можно интерпретировать так: совокупность отклонений в n–мерном пространстве переменных x1…xn определяет точку М (изображающая точка). В возмущенном движении при изменении в-н x1…xn, М будет описывать некоторую траекторию. Невозмущенному движению xj = 0 отвечает неподвижная точка – начало координат.
Мера отклонения: 
При t = t0 xj=x0j=ε j(j=1..n), т.е. начальные значения отклонений xojпредставляют возмущения системы (8)
Определение устойчивости движения по Ляпунову.
Если по любому положительному числу ε, как бы оно не было мало, можно найти такое положительное число δ, что при всяких возмущениях x0j, удовлетворяющих условию  (9) и при любых
(9) и при любых 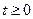 будет определяться неравенство
будет определяться неравенство  (10), то невозмущенное движение устойчиво, в противном случае нет.
(10), то невозмущенное движение устойчиво, в противном случае нет.
Практически устойчивость данного невозмущенного движения означает, что при достаточно малых начальных возмущениях, возмущенное движение будет сколь угодно мало отличаться от невозмущенного.
Если же невозмущенное движение неустойчиво, то возмущенное движение будет отходить от него, как бы малы ни были начальные возмущения.
Если невозмущенное движение устойчиво и при этом любое возмущенное движение при достаточно малых начальных возмущениях стремится к невозмущенному движению, т.е  (11), то невозмущенное движение называется асимптотически устойчивым
(11), то невозмущенное движение называется асимптотически устойчивым
Рассмотрим сферу  Выберем радиус √ ε произвольно малым. Если движение устойчиво, то для этой сферы должна найтись другая сфера
Выберем радиус √ ε произвольно малым. Если движение устойчиво, то для этой сферы должна найтись другая сфера  , обладающая следующим свойством.
, обладающая следующим свойством.
Изображающая точка М, начав свое движение из любого положения М0, лежащего внутри или на поверхности сферы δ, при своем дальнейшем движении остается всегда внутри сферы ε, никогда не достигая ее поверхности.
Если же невозмущенное движение неустойчиво, то хотя бы одна траектория изображающей точки М с течением времени пересечет сферу ε изнутри наружу при сколь угодно близком положении точки М0 к началу координат.
Геометрически это означает, что при асимптотической устойчивости изображающая точка должна неограниченно стремится к началу координат, не выходя из сферы ε.
В тех случаях, когда асимптотическая устойчивость имеет место при любых возмущениях (не обязательно малых), невозмущенное движение называется асимптотически устойчивым в целом. Иногда устойчивость имеет место не при любых возмущениях, а при возмущениях, подчиненных некоторым условиям. Такая устойчивость называется условной.
Особенности определения устойчивости по Ляпунову.
1. Возмущения накладываются только на начальные условия, что физически говорит о том, что возмущенное движение происходит при тех же источниках энергии, что и невозмущенное.
2. Устойчивость рассматривается на бесконечно большом интервале времени.
3. Возмущения предполагаются малыми.
Тем не менее, методы развитые Ляпуновым лежат в основе исследования других видов устойчивости движения.
Инвариантность систем.
Инвариант – отображение φ рассматриваемой совокупности М математических объектов, снабженной фиксированным отношением эквивалентности ρ, в другую совокупность N математических объектов, постоянное на классах эквивалентности М по ρ. Концепция инвариант является одной из важнейших в математике, поскольку изучение инварианта непосредственно связано с задачами классификации объектов того или иного типа.
Проблема инвариантности.
Это проблема определения таких структур и параметров систем управления, при которых влияние некоторых произвольно меняющихся внешних воздействий и собственных параметров системы на динамические характеристики процессов управления могут быть частично или полностью компенсированы.
Более простая постановка – требуется сделать по возможности независимой ту или иную переменную (обобщенную координату) от одного или нескольких внешних воздействий.
Рассмотрим линейную стационарную систему с тремя степенями свободы, состоящую из
- объекта регулирования с регулируемой координатой х1(t)
- регулятора с двумя обобщенными координатами х2(t) и х3(t)
а11x1(t)+ а12x2(t)+ а13x3(t)=f1(t) – возмущенное воздействие на объект
а21x1(t)+ а22x2(t)+ а23x3(t)=g(t) – управляющее воздействие
а31x1(t)+ а32x2(t)+ а33x3(t)=f3(t) – возмущение на регулятор
aij=mijp2+lijp+rij, где; i, j=1, 2, 3 р = d/dt
Допустим, что функция удовлетворяет требованиям оригинала, и перейдем от дифференциальных уравнений к уравнениям алгебраическим с помощью преобразования Лапласа.
структура системы

Упорядоченность системы заключается в том, что порядковый номер уравнения соответствует номеру обобщенной координаты, для которой это уравнение составлено. Поэтому элементы главной диагонали операторной матрицы (р) представляют собой собственные (характеристические) операторы каждой из обобщенных координат схемы. Остальные операторы отражают воздействие одних обобщенных координат на другие.