Моделирование и подобие. Получение критериев подобия с помощью метода интегральных аналогов (пример с уравнением Навье-Стокса)

M = v/a - число Маха, отношение скорости объекта к скорости звука.

Если М< 1, то работает докритическое течение.

При М> 1 происходят скачки уплотнения.

М=1 - граница между событиями, надкритическое течение.

Докритическое и надкритическое течения качественно отличаются.

Методы получения критериев подобия. Метод основан на использовании:

а). p - теоремы (теоремы Букингема)

б). Метода интегральных аналогов

В основе лежит теория размерности. A = {A}[A]

[A] - единицы размерности, т.е. A = {30}[км/час]

Есть единицы основные и произвольные.

Метод интегральных аналогов.
Для получения критериев подобия по методу интегральных аналогов необходимо знать уравнения системы или процесса.
Если все члены уравнения разделить на один из них, то получим уравнение в безразмерной форме (Фурье - все члены уравнения имеют одну и ту же размерность).
Пример Уравнение Навье-Стокса.
V- скорость потока в точке. F - объемная или массовая сила Р – давление r - плотность жидкости n - кинетическая вязкость Δ - лапласиан или дифференциальный оператор второго порядка Ñ - оператор набла
Δ =Ñ ´ Ñ - скалярное произведение

(их 3 для х, у и z)

-старая координата

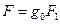
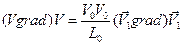
а). Пренебрегаем индексом 1
б). Разделим члены уравнения на

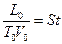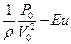- число подобия Струхаля; - число подобия Фруда; - число подобия Эйлера; - число подобия Рейнольдса