Прямой метод Ляпунова

Прямой метод Ляпунова, который позволяет судить об устойчивости непосредственно по уравнениям возмущенного движения, не прибегая к их интегрированию.

Уравнения возмущенного движения записываются в нормальной форме Коши в отклонениях от невозмущенного движения dxi/dt = Xi(x1, x2…xn) i=1…n.

Невозмущенному движению при этом соответствует тривиальное решение, т.е. x1=x2=..xn=0.

Если Xi(x1…xn) представляют собой функции фазовых координат (отклонений), непрерывные в некоторой области Rn, содержащей начало координат и имеющей частные производные по всем аргументам, то для анализа устойчивости невозмущенного движения могут быть использованы специальные функции фазовых координат, называемые функциями Ляпунова.

Прямой метод опирается на известную теорему Лагранжа, согласно которой равновесие устойчиво, если в положении равновесия потенциальная энергия системы минимальна.

Идея метода состоит в том, чтобы подобрать такую функцию фазовых координат, которая бы в некотором смысле была аналогична потенциальной энергии системы в состоянии покоя.

Рядом специальных свойств обладают функции Ляпунова. Это непрерывные однозначные функции фазовых координат, определенные в области RnΣ xj2≤ μ (15) (μ - постоянное положит. число), удовлетворяющие условию V(x1…xn)=0 при x1=x2=…xn=0 (16) и имеющие производные по всем аргументам. Цель состоит в том, чтобы, предполагая невозмущенное движение устойчивым, попытаться подобрать такую функцию фазовых координат, которая при любом движении системы уменьшалась, т.е dV/dt< 0.

Если в окрестности начала координат функция V кроме нуля может принимать значения только одного знака, то она называется знакопостоянной.

Если знакопостоянная ф-я обращается в нуль только в том случае, когда все x1…xnравны нулю, то ф-я V называется знакоопределеной.

Знакоопределенная функция имеет при x1=…xn=0 экстремум (min для опред.-положит. функции и mах для опред.-отриц). Знакопостоянная ф-я в начале координат экстремума не имеет, т.к. в окрестности начала координат есть точки, в которых V=0.

Пусть V=V(x) непрерывна вместе с производными первого порядка: кроме того предположим, что V(x) знакоопределенная.
Тогда при x1=…xn=0 она будет иметь изолиров. экстремум и все

Разложим V в ряд Маклорена по степеням x1…xn

Учитывая (16) и (17), получим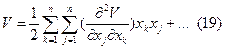

Обозначим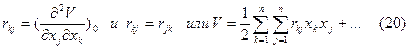

Т.о. разложение знакоопределенной функции V в ряд по степеням x1…xn не содержит членов первой степени, т.е. остается квадратичная форма:

Пусть квадратичная форма принимает положительные значения и в нуль обращается только при x1=…xn=0. Тогда вне зависимости от членов высшего порядка при достаточно малых по модулю xj функция V будет принимать тоже положительные значения и в нуль обращается только при x1=…xn=0.
Если квадратичная форма (21) определенно – положительна, то и функция будет определенно положительной.

Рассмотрим матрицу коэффициентов квадратичной формы (21) и составим из нее n главных диагональных миноров.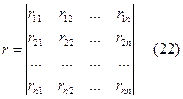

В линейной алгебре доказывается следующий критерий Сильвестра:
Для того, чтобы квадратичная форма была определенно-положительной, необходимо и достаточно, чтобы все главные диагональные миноры матрицы ее коэффициентов были положительны, т.е. Δ 1> 0, Δ 2> 0… Δ n> 0

Для того, чтобы квадратичная форма была определенно-отрицательной, необходимо и достаточно, чтобы имели место неравенства Δ 1< 0, Δ 2> 0, Δ 3< 0, т.е. oпределители должны последовательно чередовать знак, причем знак Δ 1=c11д.б. отрицательным.
Критерий Сильвестра для квадратичной части функции V является достаточным (но не необходимым) условием определенной положительности самой функции V.

Может оказаться, что разложение знакоопределенной функции V в ряд по степеням x1…xn начинается не с членов второго, а с членов более высокого порядка. В этом случае общих приемов исследования функции на знакоопределенность нет.