Основные определения

Фракталы, определение и примеры

Абстрагируясь от специфической природы систем, синергетика может описывать их эволюцию на интернациональном языке, устанавливая своего рода изоморфизм двух явлений. Фрактальные модели, как и природные объекты, обладают «шероховатостью», и свойство это сохраняется при сколь угодно большом увеличении модели.

Основные определения

Геометрические модели различных природных конструкций традиционно строятся на основе простых геометрических фигур. Этот набор плохо применим для характеристики сложных объектов, таких как очертание береговых линий материков, поле скоростей в турбулентном потоке жидкости, и. т. д.. Для описания таких систем используются фракталы. Основой новой геометрии является идея самоподобия. Она выражает собой тот факт, что иерархический принцип организации фрактальных структур не претерпевает значительных изменений при рассмотрении их через микроскоп с различным увеличением. В результате эти структуры на малых масштабах выглядят в среднем также как и на больших. Фрактальная кривая, даже на самом маленьком масштабе не сводится к прямой и является в общем случае геометрически нерегулярной, хаотичной. Для нее не существует понятия касательной к точке, так как функции, описывающие эти кривые, являются в общем случае недифференцируемы.

Фрактальная геометрия необходима, например, при изучении поглощения или рассеяния излучения в пористых средах, для характеристики сильно развитой турбулентности, при моделировании свойств поверхности твердых тел, и. т. д..

Фракталы – это геометрические объекты: линии, поверхности, пространственные тела, имеющие сильно изрезанную форму и обладающие свойством самоподобия.

фрактал –обозначает множество, имеющее дробную фрактальную размерность. Для пояснения фрактальной размерности необходима топологическая размерность. Под топологической размерностью Dt множества в линейном пространстве понимают число линейно независимых координат в пространстве. Например, окружность и линия имеют топологическую размерность 1; круг и квадрат – 2; шар и куб – 3. Фрактальная размерность множества D – размерность того пространства, которое полностью заполняется множеством. Для связи фрактальной и топологической размерностей используют показатель Херста – Н, вычисляемый по формуле: H = D – Dt.

Существует два способа построения фракталов. Первый способ – это использование Систем Итерированных Функций (СИФ). Второй способ – это использование L-систем, названных так в честь ученого Астрида Линденмайера. С их помощью можно строить многие известные самоподобные фракталы.

L-система – это грамматика языка, которая описывает инициатор и преобразование, выполняемое над ним.

Процесс построения фрактала с помощью L-системы.

1. Задается аксиома (сценарий по которому будет рисовать черепашка);

2. Задается набор порождающих правил (указывают как будет изменяться аксиома от итерации к итерации);

3. Задается начальный угол построения и величина угла приращения;

4. Задается количество итераций (количество шагов);

5. Запуск процесса построения.

Фракталы и математический хаос – подходящие средства для исследования сложных и нерегулярных систем, таких как, например каскадные и турбулентные процессы.

Разделим отрезок прямой на N равных частей. Тогда каждую часть можно считать копией всего отрезка, уменьшенной в 1/r раз. Очевидно, N и r связаны соотношением Nr = 1. Если квадрат разбить на N равных квадратов (с площадью, в 1/r² раз меньше площади исходного), то соотношение запишется как Nr² = 1. Если куб разбить на N равных кубов (с объемом, в 1/ r³ раз меньше объема исходного), то соотношение примет вид Nr³ = 1. Заметим, что размерность d объекта, будь то одномерный отрезок, двумерный квадрат или трехмерный куб, появляется как степень r в соотношении между N, числом равных подобъектов, и коэффициентом подобия r.

А именно: *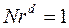

Множество в котором показатель d в равенстве (*) не является целым, то есть такое, что при разбиении исходного множества на N непересекающихся подмножеств, полученных масштабированием оригинала с коэффициентом r, значение d не будет выражаться целым числом, называют самоподобным фракталом. Величину d называют фрактальной (дробной) размерностью или размерностью подобия. Явное выражение для d через N и r находится логарифмированием обеих частей:

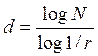
Логарифм можно взять по любому положительному основанию, отличному от единицы, например по основанию 10 или по основанию e» 2, 7183.