
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нечеткое представление информации; типовые функции принадлежности, мера нечеткости.
|
|
Степень принадлежности к множеству A, представляющая собой обобщение характеристической функции, называется функцией принадлежности.
Значения функции принадлежности являются рациональными числами из интервала [0, 1], где 0 означает отсутствие принадлежности к множеству, а 1 - полную принадлежность.
На нечетких множествах, рассматриваемых как обобщение обычных множеств, можно определить ряд математических операций, являющихся обобщением аналогичных операций, выполняемых на " четких" множествах. К ним относятся:
1. Логическая сумма множеств 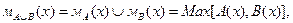
2. Логическое произведение множеств 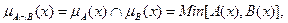
3. Отрицание множества 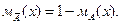
4. Равенство множеств А и В
Нечеткие множества А(х) и В(х) равны между собой, когда для всех элементов Xi обоих множеств выполняется условие 
Для определения степени нечеткости множества введено понятие меры нечеткости.
Наиболее популярна мера Р.Егера, в соответствии с которой степень нечеткости множества А в метрике р, определяется выражением
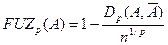
Нечеткость и вероятность
В теории вероятности событие u либо происходит, либо нет, а вероятное p(u) представляет меру того, что оно состоится или что случайная переменная x примет значение u.
Понятие нечеткости измеряется степенью, с которой событие x=u принадлежит к некоторому множеству событий А. Фактически измеряется степень, в которой универсальное множество U содержится в подмножестве A.