
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Считаем дискриминантные функции
|
|
8. Оцениваем достоверность. Для этого считаем вероятность, соответствующую наибольшей дискриминантной функции  ; fL– значение наибольшей дискриминантной функции
; fL– значение наибольшей дискриминантной функции
L – индекс наибольшей дискриминантной функции
26.Метод Бокса- Уилсона.
Идея метода заключается в использовании метода крутого восхождения в сочетании с последовательно планируемым факторным экспериментом для нахождения оценки градиента.
Процедура состоит из нескольких повторяющихся этапов:
- построение факторного эксперимента в окрестностях некоторой точки;
- вычисление оценки градиента в этой точке по результатам эксперимента;
- крутое восхождение в этом направлении;
- нахождение максимума функции отклика по этому направлению.
Допущения:
- функция отклика непрерывна и имеет непрерывные частные производные на множестве G;
- функция унимодальная (т.е. экстремум - внутренняя точка).

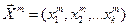
m – номер итерации

α влияет на шаг.
 - оператор Набла
- оператор Набла
 Δ х нужно подсчитать
Δ х нужно подсчитать
Пример (на градиентный метод)
max f(x) = 4x1+ 2x2- x12- x22+5
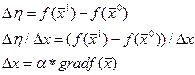 |
 = (4, 5) - исходная точка.
= (4, 5) - исходная точка. - общий вид
х2
х1

¶f/¶x1= 4 - 2x1
¶f/¶x2= 2 - 2x2
Ñ f(x0) = (4-2*4, 2-2*5) = (-4, -8) - градиент в точке x0

Вторая итерация

т.е. точка
 - решение задачи
- решение задачи
Оценивание градиента.
Если функция h(x1, x2,..., xk), где x1, x2,..., xk- размерные величины, то перейдем к безразмерному виду: f(x1, x2,..., xk), где x1, x2,..., xk- безразмерные величины.
Разложим эту функцию в ряд Тейлора в точке 0.

Для линейной зависимости.
f(x1, x2,..., xk) = a0+ a1x1+ a2x2+...+ akxk
где ai= ¶f/¶xi i = 1…k i ¹ 0
a0= f(x10, x20,..., xk0)0

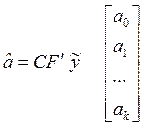 - из регрессионной модели
- из регрессионной модели  - из разложения в ряд Тейлора
- из разложения в ряд Тейлора
Проведя факторный эксперимент и рассчитав коэффициент линейной множественной регрессионной модели, мы получаем возможность оценить компоненты градиента.
25.Планирование эксперимента. Основные понятия.






 - Активный эксперимент
- Активный эксперимент
- Пассивный эксперимент
Основная идея активного эксперимента - добиться требуемых свойств, выбирая условия проведения эксперимента.
1. План эксперимента X
1 £ j £ n 1 £ i £ N
n - число факторов, N - число экспериментов
xi= (x1i, x2i,..., xni)¢
x11, x21,..., xn1
X = xji= x12, x22,..., xn2
......
x1N, x2N,..., xnN
2. Центр плана
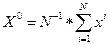
.. +1, -1
..
3. Центральный план
- это план, в котором центр расположен в начале координат.
4. Область определения. Нормированные переменные.
Пусть
xj*- реальные факторы
xj- нормированные факторы
-1£ xj£ 1 1£ j £ n n - факторы
Надо определить xj*min и xj*max
xj= [xj*- (xj*min+ xj*max)/2] / [(xj*max- xj*min)/2]
5. Матрица M = F¢ F
y = a0+ a1x1+ a2x2+... + anxn

М - информационная матрица плана X размерности (k+1)*(k+1)
det(A-l I) = 0 где l- корни характеристического уравнения.
M=(Матрица у которой на диогонале числа, а все остальное нули)
План X, которому соответствует диагональная информационная матрица, называется ортогональным.
Если при применении МНК какие-либо коэффициенты а оказываются незначимыми, то в общем случае необходимо произвести перерасчет коэффициентов для новой модели.
Если использовался критерий ортогональности плана, то замена на 0 любого коэффициента в уравнении модели не изменит оценок других коэффициентов.
Преимущества ортогонального плана:
а) упрощение вычислений
б) независимые коэффициенты оценок
6. Свойство ротатабельности
План X является ротатабельным, если дисперсия оценки  зависит только от расстояния точки x от центра плана.
зависит только от расстояния точки x от центра плана.
Пример Пусть модель y(a, x) = a0+ a1x1+ a2x2+... + anxn
x0= 0 - центр плана
 M = 4I3
M = 4I3 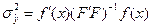
f(x) = (1, x1, x2)
 = (1, x1, x2)*(1/4)I3
= (1, x1, x2)*(1/4)I3  = (1/4)(1+ x12+ x22) =
= (1/4)(1+ x12+ x22) =
= (1/4)(1+r2)
Дисперсия всех равноудаленных точек одинакова.
7. План X называется ненасыщенным, если N > k+1;
насыщенным, если N = k+1
8. Критерий планирования эксперимента.
План эксперимента зависит от выбранного критерия. Критерий в основном определяет либо требования к модели, либо требования к точности.
Кроме критериев ортогональности и ротатабельности назовем критерии А-оптимальности и Д-оптимальности.
Критерий А-оптимальности требует такого выбора плана X, при котором матрица C имеет минимальный след (т.е. сумма диагональных элементов минимальна). Практически это означает минимизацию средней дисперсии оценок коэффициента а.
Критерий D-оптимальности требует такого расположения точек, при котором определитель матрицы C минимален.