
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матричная форма МНК при построении модели (этап проверки адекватности полученной модели).
|
|
Виды регрессий.
1. Линейный одномерный случай
y = a0+ a1x
2. Параболическая или степенная регрессия 
 3. Линейная множественная регрессия
3. Линейная множественная регрессия 
x1,..., xn y


факторы функция отклика
y(a, x) = a0+ a1x1+...+ anxn+ an+1x12+...+ a2nxn2+ a2n+1x1x2+...+ akxn-1xn
k+1 = (n+1)(n+2)/2
- число неизвестных 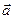 =?.
=?.
МНК имеет три этапа:
1 этап Определение коэффициентов а.
2 этап Оценка достоверности коэффициентов а.
3 этап Проверка адекватности модели.
 Проверка адекватности модели.
Проверка адекватности модели.
Н0: tр£ tкр
где tр- расчетное значение; tкр- табличное значение
1- a = р
a
В основе проверки адекватности модели лежит сопоставление достигнутой точности модели с точностью наблюдения. Для оценки точности используем дисперсию, поэтому необходимо сравнить дисперсию ошибки по модели с дисперсией ошибки наблюдений. Поэтому в каждой точке эксперимент повторяется n раз.
 отсюда следует, что
отсюда следует, что 
1.Дисперсия ошибки моделирования. 
2. Дисперсия ошибки наблюдения 
 Далее рассчитываем статистику Фишера Fр= (SD/j1)/(Se/j2). Если ошибка моделирования меньше ошибки наблюдения, то модель хорошая. Выдвигается гипотеза Н0. Определяется уровень значимости a.
Далее рассчитываем статистику Фишера Fр= (SD/j1)/(Se/j2). Если ошибка моделирования меньше ошибки наблюдения, то модель хорошая. Выдвигается гипотеза Н0. Определяется уровень значимости a.
В соответствии с a, j1и j2из таблицы находим Fкр.
P{ï Fï < Fкр} = 1-a
fF
F
Fp Fкр
Если Fp£ Fкр, то модель адекватна.