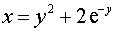Линейные уравнения первого порядка

Дифференциальное уравнение первого порядка называется линейным, если оно имеет следующий вид:

(1)

Если 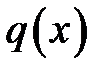=0, то уравнение называется линейным однородным дифференциальным уравнением – ЛОДУ, иначе линейным неоднородным дифференциальным уравнением – ЛНДУ.

Рассмотрим сначала ЛОДУ 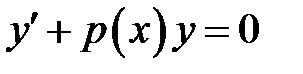. Оно является уравнение с разделяющимися переменными.

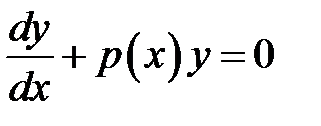
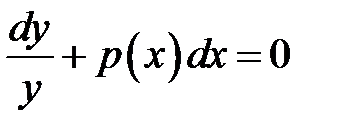
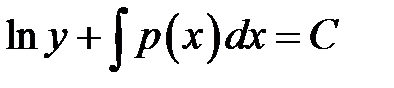
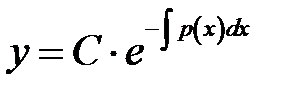
План решения.

Способ 1. Метод Бернулли.

Ищем решение уравнения (1) в виде:

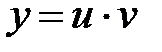, (2)

где u и v – неизвестные функции x.

Уравнение (1) принимает вид

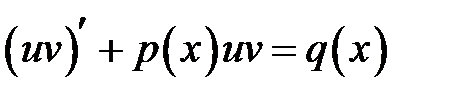
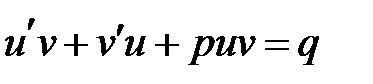
Преобразуем уравнение к виду

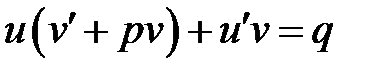
и полагаем скобку равную нулю. Это не сужает множество решений, т.к. уравнение содержит две неизвестные функции. Получим систему:

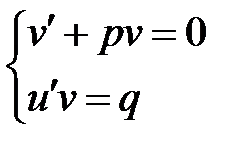
Решаем первое уравнение системы и находим функцию v (константу С не пишем).

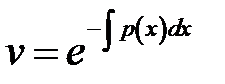
Подставляем найденное значение v во второе уравнение системы и находим функцию u (появляется константа С).

Записываем общее решение уравнения (1) в виде .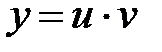

Способ 2. Используя метод вариации произвольной постоянной.

Записываем соответствующее однородное линейное уравнение:

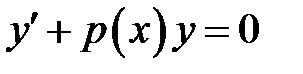. (2)

Это уравнение с разделяющимися переменными.

Разделяя переменные и интегрируя, получим общее решение однородного уравнения (2):

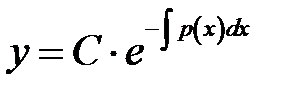. (3)

Применяем метод вариации произвольной постоянной.

а) ищем решение неоднородного уравнения (1) в виде (3), считая С неизвестной функцией от х, т.е. полагая С=С(х);

(4)

б) подставляем в уравнение (1) y и y’, определяемые из соотношения (4). Из полученного дифференциального уравнения определяем функцию C(x).

Общее решение неоднородного уравнения получаем в виде (4)

Здесь C(x) содержит произвольную постоянную C₀.

Замечание. Иногда бывает удобным представить x как функцию от y, т.е. x=x(y).

Утверждение. Линейное однородное уравнение имеет линейное пространство решений.

Пример 1. Найти решение задачи Коши.

.

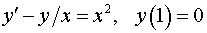Способ 1.

Полагаем 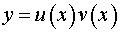. Тогда .

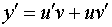Получаем

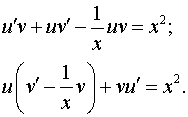
Пусть 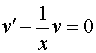. Тогда

.

.

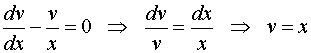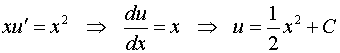Общее решение исходного уравнения:

.

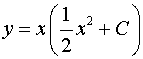Используя начальное условие, находим решение задачи Коши.

.

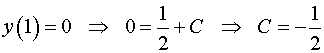Частное решение:

.

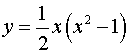Способ 2.

Решим соответствующее однородное уравнение:

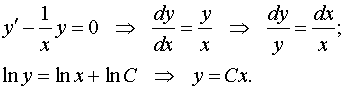
Полагаем 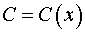и подставляем в исходное уравнение.

.

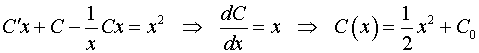Тогда

.

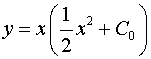Используя начальное условие, находим решение задачи Коши.

.

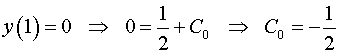Частное решение:

.

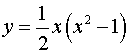Пример 2. Найти решение задачи Коши. Удобнее найти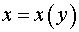

.

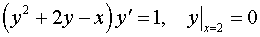Преобразуем уравнение к следующему виду, считая 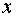функцией от .

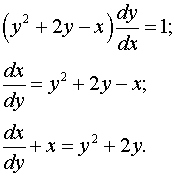
Способ 1.

Полагаем 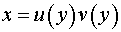. Тогда .

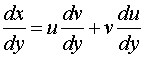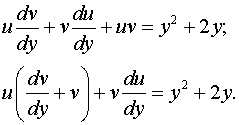
Пусть 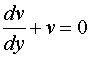. Тогда

.

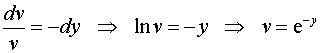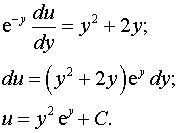
Общее решение исходного уравнения:

.

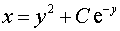Используя начальное условие, находим решение задачи Коши.

.

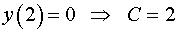Частное решение:

.

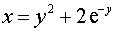Способ 2.

Решим соответствующее однородное уравнение.

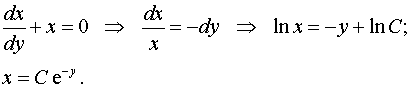
Полагаем 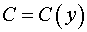и подставляем в исходное уравнение.

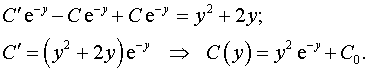
Общее решение:

.

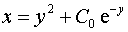Используя начальное условие, находим решение задачи Коши.

.

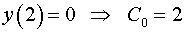Частное решение: