
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коэффициент корреляции его свойства
|
|
Значение корреляционного момента  зависит от единиц измерения СВ
зависит от единиц измерения СВ  и
и  . Безразмерным аналогом
. Безразмерным аналогом  является коэффициент корреляции, определяемый формулой:
является коэффициент корреляции, определяемый формулой:
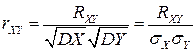 ,
,
где 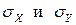 - средние квадратические отклонения СВ
- средние квадратические отклонения СВ  и
и  .
.
Свойства коэффициента корреляции.
1. 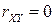 , если СВ
, если СВ  и
и  являются независимыми.
являются независимыми.
(Свойство очевидно, так как в этом случае 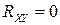 ).
).
2. Коэффициент корреляции по модулю не превосходит 1: 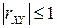 .
.
▲ В соответствии со свойством 1 дисперсии
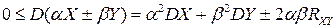 .
.
Положим 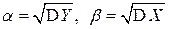 . Тогда
. Тогда
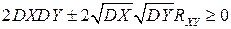 ,
,
откуда
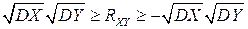 .
.
Следовательно,
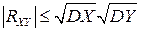 , или, эквивалентно,
, или, эквивалентно, 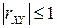 .■.
.■.
3. 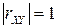 тогда и только тогда, когда СВ
тогда и только тогда, когда СВ  и
и  связаны линейной зависимостью, то есть существуют действительные числа А и В такие, что
связаны линейной зависимостью, то есть существуют действительные числа А и В такие, что 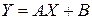 .
.
▲ Необходимость. Предположим, что 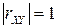 . Тогда
. Тогда 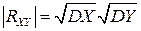 и из доказательства свойства 2 коэффициента корреляции следует, что
и из доказательства свойства 2 коэффициента корреляции следует, что 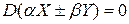 при
при 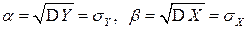 . В соответствии со свойством 1 дисперсии это означает, что
. В соответствии со свойством 1 дисперсии это означает, что 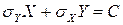 , откуда
, откуда 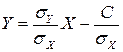 и значит
и значит 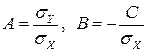 .
.
Достаточность. Пусть 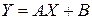 . Тогда
. Тогда 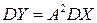 , а корреляционный момент СВ
, а корреляционный момент СВ  и
и  равен
равен
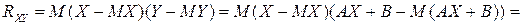
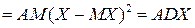 .
.
Поэтому 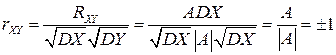 ■.
■.
Итак, 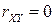 для независимых СВ и достигает максимального по модулю значения
для независимых СВ и достигает максимального по модулю значения 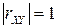 для сильно (линейно) зависимых СВ. Поэтому значение коэффициента корреляции можно интерпретировать как степень линейной зависимости между СВ.
для сильно (линейно) зависимых СВ. Поэтому значение коэффициента корреляции можно интерпретировать как степень линейной зависимости между СВ.
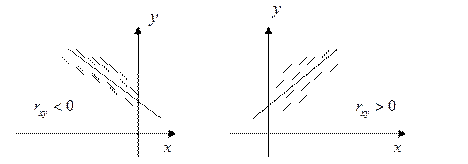 |
Геометрическая иллюстрация: чем больше по модулю
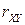 , тем плотнее значения
, тем плотнее значения 
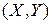 располагаются вдоль некоторой прямой.
располагаются вдоль некоторой прямой.
Многомерный случай.
Основными числовыми характеристики 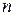 -мерного
-мерного 
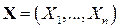 являются:
являются:
· математическое ожидание 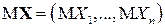 ;
;
· корреляционная матрица 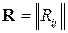 , элементами которой являются всевозможные попарные корреляционные моменты координат:
, элементами которой являются всевозможные попарные корреляционные моменты координат: 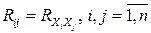 .
.
Свойства корреляционной матрицы.
1. Матрица 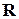 является симметрической размера
является симметрической размера 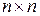 :
: 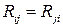 ,
, 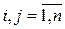 .
.
2. На диагонали матрицы 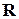 расположены дисперсии координат
расположены дисперсии координат 
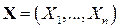 :
: 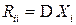 ,
, 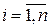 .
.
3. Матрица 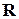 является неотрицательно определенной матрицей, то есть для любого
является неотрицательно определенной матрицей, то есть для любого 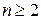 и для любых действительных чисел
и для любых действительных чисел 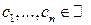
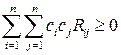 .
.
▲ Обозначим 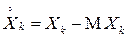 - центрированную СВ,
- центрированную СВ, 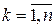 . Тогда
. Тогда 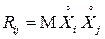 и для произвольных чисел
и для произвольных чисел 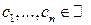 имеем:
имеем:
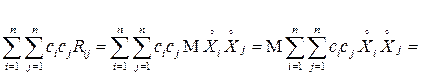
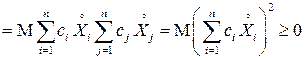 ■.
■.
Наряду с корреляционной матрицей 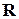 , иногда рассматривают нормированную корреляционную матрицу
, иногда рассматривают нормированную корреляционную матрицу 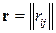 , элементами которой являются всевозможные попарные коэффициенты корреляции координат:
, элементами которой являются всевозможные попарные коэффициенты корреляции координат: 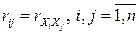 . Отличие ее от просто корреляционной матрицы состоит в том, что у нормированной корреляционной матрицы все диагональные элементы равны 1:
. Отличие ее от просто корреляционной матрицы состоит в том, что у нормированной корреляционной матрицы все диагональные элементы равны 1: 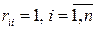 .
.