Многомерное нормальное (гауссовское) распределение

Нормальное распределение в одномерном случае задается ПВ вида:

,

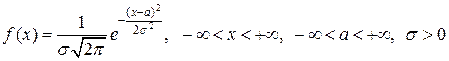причем параметры 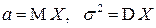(предполагается, что , иначе распределение является вырожденным).

Определение. Говорят, что 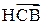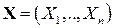имеет многомерное нормальное (гауссовское) распределение, если его ПВ имеет вид:

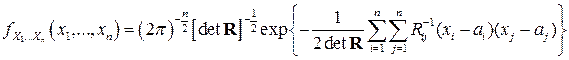, (3.19)

где 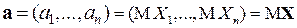- математическое ожидание 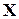; 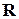- корреляционная матрица 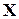; 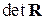- определитель корреляционной матрицы 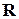(предполагается, что 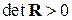); 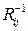– алгебраическое дополнение к элементу 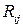матрицы 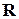(так, что 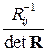- элемент матрицы, обратной к ).

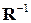Несколько более компактно выглядит запись для многомерной нормальной ПВ в векторной форме:

,

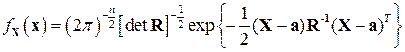где верхний индекс «Т» означает знак транспонирования.

Далее будет использоваться для нормального краткая запись: .

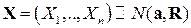Из выражения (3.19) для ПВ видно, что нормальный закон распределения полностью определяется моментами первых двух порядков: математическими ожиданиями 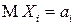, дисперсиями 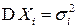и корреляционными моментами .

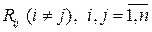Если 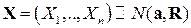и его координаты являются попарно некоррелированными СВ, то есть 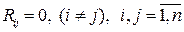, то корреляционная матрица 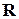и обратная к ней 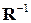являются диагональными

, .

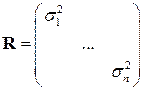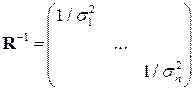Поэтому из (3.19) следует, что

,

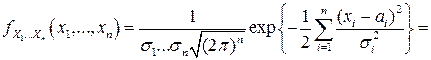
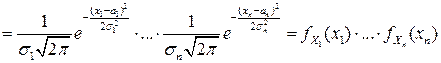где 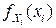- ПВ одномерного нормального распределения с параметрами 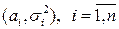. Но это означает независимость СВ .

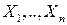Таким образом, для нормально распределенных СВ понятия независимости и некоррелированности совпадают (эквивалентны).

Другие замечательные свойства многомерного нормального распределения.

Если 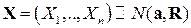, то:

1. Все координаты 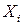имеют одномерные нормальные распределения: 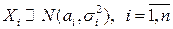(уметь доказывать при ).

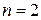2. Все условные ЗР являются нормальными (уметь доказывать при ).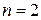

3. Если координаты 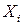являются независимыми СВ, то любая их линейная комбинация 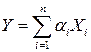также является нормальной СВ: 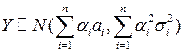(уметь доказывать при 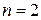с помощью интеграла свертки).

Рассмотрим подробнее случай . Пусть - , у которого 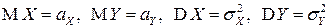. В этом случае корреляционная матрица имеет вид: 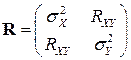, а определитель корреляционной матрицы .

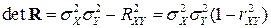Поэтому ПВ двумерного нормального имеет вид:

.

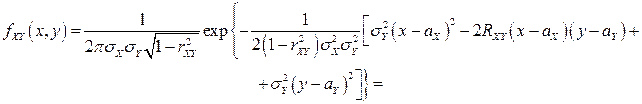
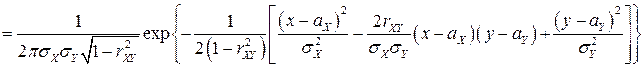Для двумерного нормального используется краткая запись: 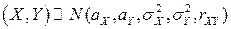(зависит от пяти параметров).

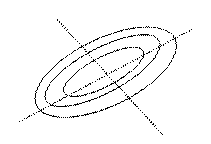
График двумерной ПВ имеет вид:

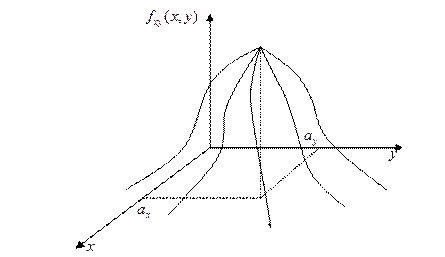
Линиями уровня являются эллипсы:

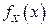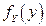Найдем одномерные ПВ и координат .

,

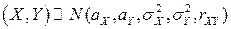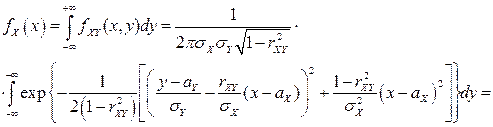
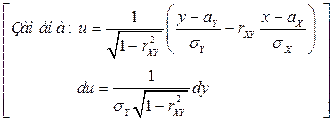
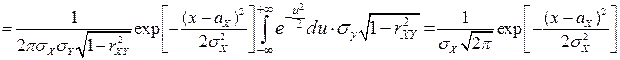то есть .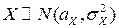

Аналогично, 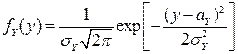, то есть .

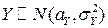Таким образом, у двумерного нормального одномерные законы распределения всегда являются нормальными.

Найдем условные ЗР, если .

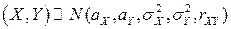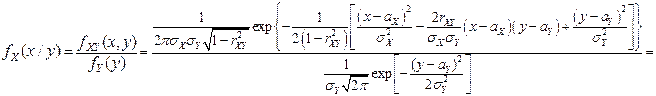
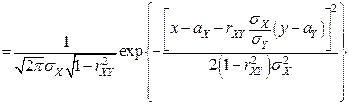
Из полученного вида условной ПВ 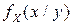следует, что она является ПВ нормального ЗР с параметрам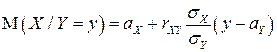и

и .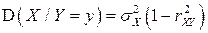

Полностью аналогично получаем, что условная ПВ

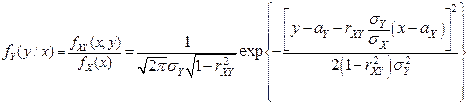
является ПВ нормального ЗР с параметрам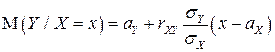и

и .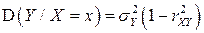

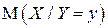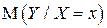Таким образом, если - двумерный нормальный , то условные математические ожидания и являются линейными функциями условия (или, другими словами, в нормальном случае уравнения регрессии являются линейными), а условные дисперси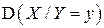и и 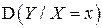являются постоянными величинами.