Решение. Задача может быть решена как с помощью интегрального преобразования Фурье, т.е

Задача может быть решена как с помощью интегрального преобразования Фурье, т.е. с использованием понятий спектральной плотности стационарного процесса S_XX (w) и передаточной функции линейной системы H (j w), так и с помощью двустороннего преобразования Лапласа, т.е. с применением S_XX (p) и Н (p).

Спектральная плотность стационарного эргодического случайного процесса X (t) связана с корреляционной функцией этого процесса с помощью соотношений Винера-Хопфа, полученных на основе двойного интеграла Фурье:

S_XX (w) =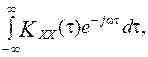

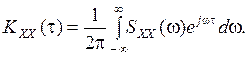
При использовании двустороннего интегрального преобразования Лапласа приведенные соотношения принимают вид:

S_XX (p) = 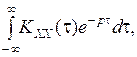(2.1)

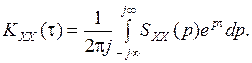(2.2)

Корреляционная функция K_XX(t) при использовании последнего выражения может быть определена с помощью теории вычетов:

K_XX (t) = 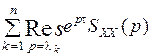при 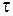> 0, (2.3)

K_XX (t) = при t< 0, (2.4)

где

l _к и m _к - левые и правые полюса S_XX (p), соответственно.

Дисперсия процесса X (t) определяется по выражениям (2.2)…(2.4) при t=0: D_X = K_XX (0).

В рассматриваемом примере

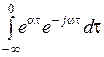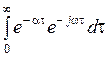S_XX (w) = D_X + D_X = (2.5)

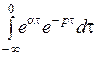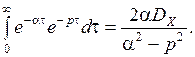S_XX (p) = D_X + D_X (2.6)

Следует отметить, что выражение (2.5) может быть получено из выражения (2.6), если в последнем положить p = j w.

Передаточную функцию схемы рис.2.1 получим, используя одностороннее интегральное преобразование Лапласа и полагая, что случайный процесс X (t) представляет собой напряжение на входе схемы. Тогда

H (p)= Y (p)/ X (p)= I (p) R ₂, (2.7)

где I (p)= X (p)/(R ₂+ R ₁+ pL) – операторное изображение тока. (2.8)

Подставляя (2.8) в (2.7), получим

H (p)= R ₂/(R ₁+ pL)=d₂/(p +d), (2.9)

где d₂= R ₂/ L, d=(R ₁+ R ₂ )/L – декремент контура (d=1/ T, T – постоянная времени контура.

Спектральная плотность случайного процесса на выходе схемы определится как

S_YY (p)= S_XX (p)× H (p)× H (- p) = 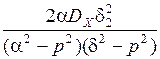(2.10)

или

S_YY (w)= S_XX (w)× × H (j w) H (- j w) = 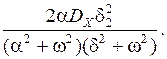(2.11)

Для определения корреляционной функции случайного процесса Y (t) воспользуемся выражениями (2.3), (2.4) и (2.10). Спектральная плотность S_YY(p) имеет два левых полюса p ₁=-a и p ₂=-d и два правых полюса p₁=a и p ₂=d. Беря с помощью второй теоремы разложения Хевисайда оригиналы изображений (2.3) и (2.4) , получим

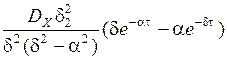
K_YY (t) = при t> 0, (2.12)

K_YY (t) = 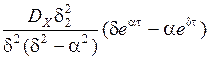при t < 0. (2.13)

Объединяя выражения (2.12) и (2.13), получим:

K_YY (t) = при 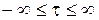. (2.14)

Дисперсия стационарного процесса на выходе схемы рис.1 определится как

D_Y = K_YY (0) = D_X 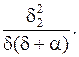(2.15)