Решение. 1. Изобразить на рисунке линии индукции электрического поля, созданного данным заряженным телом.

Метод решения задач:

1. Изобразить на рисунке линии индукции электрического поля, созданного данным заряженным телом.

2. Выбрать форму и размер замкнутой вспомогательной поверхности, охватывающей заряд, и проходящей через точку, в которой определяется индукция.

Форма поверхности должна быть такой, чтобы линии индукции были параллельны или перпендикулярны к ней.

3. Определить величину потока F_е через выбранную поверхность

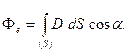
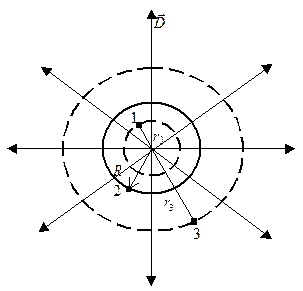
Рис.8.1

4. Определить величину заряда, охваченного выбранной вспомогательной поверхностью.

5. Приравнять поток линий индукции к величине заряда, охваченного поверхностью

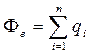
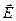6. Определить индукцию и напряжённость электрического поля.

Рассмотрим применение теоремы на примере сплошного объёмно заряженного шара (рис.8.1).

1. Линии индукции заряженного шара начинаются в его центре и являются прямыми линиями, направленными по радиусам.

2. Поле шара является сферически симметричным, вектор будет перпендикулярен любой сферической поверхности с центром в центре шара.

Следовательно, вспомогательная поверхность представляет собой сферу, проведённую через заданную точку.

3. Поток вектора индукции через выбранную сферическую поверхность

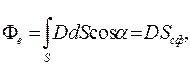
т.к. перпендикулярен сфере и совпадает с направлением нормали к ней, т. е. a = 0.

Тогда

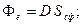
Для точки 1 (r < R) поверхностью является сфера, проходящая через точку 1 внутри шара.

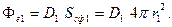
4. Заряд, охваченный этой сферой, равен 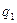= r V ₁, где 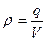- объёмная плотность заряда, т.е. заряд, приходящийся на единицу объёма.

Объём шара 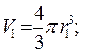Заряд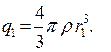

5. Приравняем поток к заряду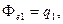

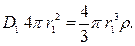
6. Находим и :

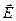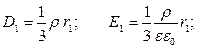
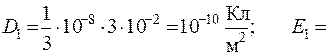~ 4 .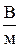

Повторим рассуждения для точек 2 и 3. Выбранные вспомогательные поверхности будут сферическими.

Точка 2. Радиус вспомогательной поверхности равен радиусу шара, т.к. точка лежит на поверхности шара ().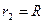

; .

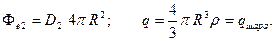
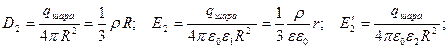
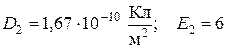
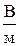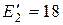
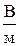На поверхности напряжённость имеет два значения Е ₂ и 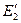, отличающиеся в e раз.