
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Структура периодического замкнутого класса
|
|
Пусть d> 1 период замкнутого класса S. Несмотря на сложность переходов внутри класса, можно обнаружить некоторую цикличность в переходах из одной группы состояний в другую. Покажем это.
Выберем некоторое начальное состояние k и определим следующие подклассы:
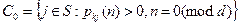 ,
,
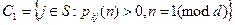 ,
,
………………………………………
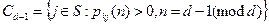 .
.
Очевидно, что S=C 0+ C 1+…+ Cd- 1. Покажем, что за один шаг система переходит из подкласса Cp в подкласс Cp+ 1, а из подкласса Cd- 1 в подкласс C 0 и так далее по этому циклу.
Пусть i Î Cp и pij> 0. Покажем, что j Î Cp+ 1.
Так как i Î Cp, то pki (n) > 0 для n = p (mod d). Тогда за число шагов n+ 1= p+ 1(mod d). система переходит в класс Cp+ 1, то есть pki (n+ 1) > 0 и что j Î Cp+ 1.
Подклассы Cp состояний периодического замкнутого класса S называются циклическими подклассами.
Из приведённых рассуждений видно, что матрицу вероятностей переходов периодического замкнутого класса можно представить в следующем виде
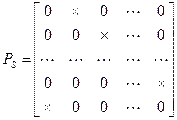 ,
,
в котором элементы матрицы, неравные нулю отмечены символом  .
.
Возвращаясь к циклическим подклассам, можно сделать вывод о том, что если в начальный момент времени система находится в состоянии подкласса C 0, то в момент времени n=1+dr, r=0, 1, 2, …, она будет находиться в подклассе C 1. Следовательно, с каждым из подклассов C 0, C 1 можно связать новую марковскую цепь с матрицей вероятностей переходов { pij (2), i, j Î Cp }, p =1, 2,, которая будет неразложимой и апериодической. Поэтому в дальнейшем при рассмотрении предельных свойств вероятностей pij (n), при n® ¥, можно ограничиться только эргодическими классами.