Цепи Маркова с дискретным временем

Пусть случайный процесс x(t) изменения во времени состояний некоторой системы принимает целочисленные значения i =1, 2, … из множества X конечного или счетного, то есть x(t)= i, x(t´)= j. Переходы из одного состояния в другое происходят через равные промежутки времени | t - t´ |=1, которые будем называть шагом.

Условные вероятности P{x(t´)= j |x(t)= i }= p_ij (t) для всех i, j Î X образуют матрицу вероятностей переходов цепи Маркова из одного состояния в другое в момент времени t.

Если вероятности переходов не зависят от момента времени t, то есть p_ij (t)= p_ij., то цепь Маркова называется однородной с матрицей вероятностей переходов за один шаг

,

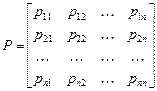где n – число состояний системы (число возможных значений цепи Маркова) – конечное или счетное. Элементы матрицы p_ij > 0 и удовлетворяют условию нормировки

, .

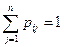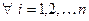Такую матрицу называют стохастической или марковской.

Набор вероятностей 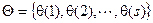, где 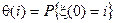называется начальным распределением, оно определяет состояние системы в начальный момент времени.

Цепь Маркова с дискретным временем полностью определяется матрицей вероятностей переходов за один шаг и начальным распределением.

Для описания цепи Маркова удобно использовать граф вероятностей переходов, вершины которого обозначают возможные состояния системы, стрелки от одной вершины к другой указывают возможные переходы между состояниями, а число над стрелкой задаёт вероятность такого перехода. Например, пусть множество состояний X={1, 2, 3} матрица вероятностей переходов имеет вид

,

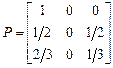тогда граф вероятностей переходов выглядит следующим образом:

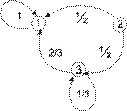
В дополнение к одношаговым вероятностям переходов интересно рассмотреть вероятности переходов из одного состояния в другое за произвольное число шагов. В силу уравнения Чепмена-Колмогорова для цепей Маркова, то есть для марковских процессов с дискретным множеством состояний, эти вероятности удовлетворяют рекуррентным соотношениям

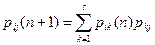, (2.2)

которые нетрудно получить, применяя формулу полной вероятности.

Обозначим через A событие, заключающееся в том, что система за (n +1) шагов перейдёт из состояния i в состояние j, через H_k – событие, состоящее в том, что за n шагов система перейдёт из состояния i в состояние k, тогда, в силу формулы полной вероятности

,

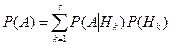обозначив

, , ,

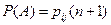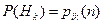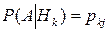можно записать равенство, совпадающее с (2.2).

Совершенно аналогично, можно получить уравнение Чепмена-Колмогорова для произвольного числа шагов n+m в виде

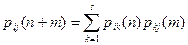, (2.3)

которое позволяет определять вероятности переходов из одного состояния в другое за произвольное число шагов. Этими формулами удобнее пользоваться, записав их в матричном виде. Так равенство (2.2) при n =1 в матричной форме имеет вид

,

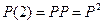тогда равенство (2.3) примет вид

.

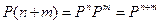Заметим, что матрицы P (n) тоже стохастические " n.

Для распределения вероятностей состояний однородной цепи Маркова имеет место следующее равенство векторов:

.

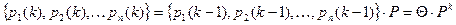Для неоднородной цепи Маркова распределение вероятностей находится по формулам

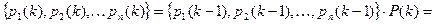
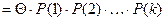
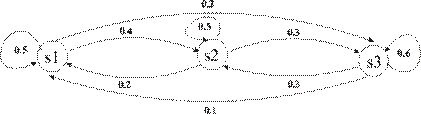
Пример 2.1. Рассмотрим состояния банка, характеризующиеся одной из процентных ставок: 12%, 13%, 14%, которые устанавливаются в начале каждого квартала и фиксированы на всем его протяжении. Таким образом, если за систему S принять действующую процентную ставку, то она в каждый момент времени может находиться только в одном из состояний: S₁ – процентная ставка 12%, S₂ – процентная ставка 13%, S₃ – процентная ставка 14%. Анализ работы банка в предшествующие годы показал, что изменение переходных вероятностей с течением времени пренебрежимо мало. Определить распределение вероятностей состояний системы в конце года, если в конце предыдущего года процентная ставка составила 13%, а граф вероятностей переходов имеет вид:

Решение. Так как множество состояний, в которых может находиться система 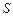, конечно, то протекающий в ней случайный процесс – дискретный. С определенной степенью погрешности можно предположить, что вероятность пребывания банка в одном из своих состояний в будущем зависит только от состояния в настоящем и не зависит от его состояний в прошлом. Поэтому рассматриваемый процесс можно считать марковским.

В силу условий банк может переходить из состояний в состояние только в определенные моменты времени 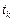– начало 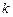-го квартала, 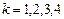, а изменение переходных вероятностей с течением времени пренебрежимо мало, то рассматриваемый процесс является однородным марковским процессом с дискретным временем.

По графу составим матрицу переходных вероятностей:

.

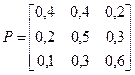Так как в конце предшествующего года процентная ставка составляла 13%, то вектор начального распределения имеет вид .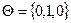

Тогда распределение вероятностей состояний процентной ставки банка в конце года, то есть по прошествии четырех кварталов определяется следующим образом:

.

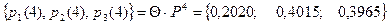Если предположить, что переходные вероятности зависят от моментов установления процентных ставок, полученный процесс будет являться неоднородной марковской цепью с дискретным временем. Например, пусть

, ,

, .

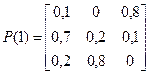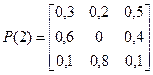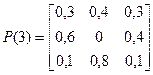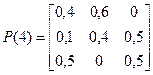Тогда 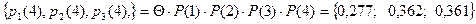.