Стационарные случайные процессы

Случайный процесс x(t) называется стационарным в узком смысле или строго стационарным, если его конечномерная функция распределения инвариантна относительно сдвига всех моментов времени t_i, i =1, 2, … n на одну и ту же величину t.

,

.

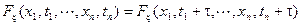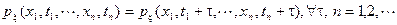Другими словами, статистические (вероятностные) свойства стационарного случайного процесса не зависят от начала наблюдения.

При n =1, из условия стационарности следует

.

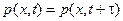Полагая t =-t, получим

,

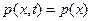то есть одномерное распределение стационарного случайного процесса не зависит от времени. А одномерное распределение определяет среднее значение и дисперсию случайного процесса, следовательно, для строго стационарного случайного процесса среднее и дисперсия не зависят от времени

,

.

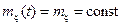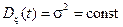При n =2, из условия стационарности, получим равенство

,

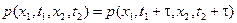полагая в котором t=– t, запишем

,

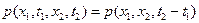то есть двумерное распределение зависит лишь от разности моментов времени, следовательно, функция корреляции стационарного случайного процесса зависит только от одного аргумента

.

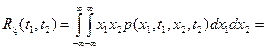
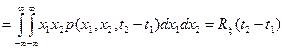Случайный процесс называется стационарным в широком смысле, если его среднее значение и дисперсия не зависят от времени, а функция корреляции зависит лишь от разности моментов времени.

Очевидно, что из стационарности в узком смысле следует стационарность в широком смысле. Обратное утверждение, вообще говоря, не верно, но для гауссовских процессов верно и обратное утверждение.