Основные определения

Марковские процессы, или процессы без последействия, являются удобной математической моделью для многих реальных процессов. Представим себе систему, которая может находиться в различных состояниях, и пусть её функционирование во времени носит стохастический характер, то есть состояния системы в момент времени t в общем случае не определяется однозначно её состояниями в предыдущие моменты s< t. Следовательно, процесс изменения во времени состояний этой системы можно описать некоторым случайным процессом x(t), заданным на интервале [0, T ] и принимающим значения из множества X.

Пусть в моменты времени t ₁< t ₂< … < t _n заданы сечения x(t ₁), x(t ₂), …, x(t_n), случайного процесса x(t). Для момента времени t _n+1> t _n рассмотрим сечение x(t_{n+ 1}) и условную функцию распределения

Интерпретируя t ₁, t ₂, …, t _n-1 как моменты времени в прошлом, t _n – настоящий (текущий) момент времени, а t _n+1 – будущий момент времени, говорят, что эта условная функция распределения характеризует функционирование системы в будущем, если известно её функционирование в прошлом и настоящее (текущее) состояние системы.

Определение. Случайный процесс x(t), называется марковским, если выполняется равенство

,

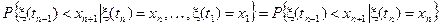то есть его условная функция распределения вероятностей значений x(t_{n+ 1}), в будущий момент времени t _n+1 не зависит от значений процесса в прошлые моменты t ₁, t ₂, …, t _n-1, а определяется лишь значением x(t _n)= x_n, в настоящий момент времени t_n.

Для условной плотности распределения записывают равенство

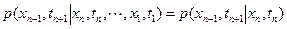, (2.1)

а условную плотность распределения p (x_{n+ 1}, t_{n+ 1} | x_n, t_n)= p (x_{n+ 1}, t_{n+ 1}; x_n, t_n)называют вероятностью перехода системы из состояния x_n в состояние x_{n+ 1} на интервале времени [ t _n, t _n+1].

Многомерную плотность распределения, в силу равенства (2.1), можно записать в виде

.

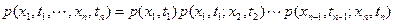Отсюда видно, что начальное распределение p (x ₁, t ₁) и вероятности переходов p (x_{n+ 1}, t_{n+ 1}; x_n, t_n) полностью определяют марковский процесс.

Вероятности переходов удовлетворяют двум основным соотношениям.

1. Условие нормировки

,

.

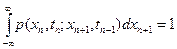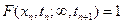2. Уравнение Чепмена-Колмогорова

.

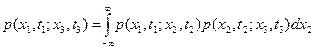Все марковские процессы можно разделить на классы в зависимости от структуры множества X – значений случайного процесса x(t), и множества моментов времени наблюдения T. Если множество X – дискретное, то процесс x(t) называется цепью Маркова.

При этом если T – дискретное, то процесс называется цепью Маркова с дискретным временем, а если T – непрерывное, то процесс называется цепью Маркова с непрерывным временем.

Если оба множества X и T непрерывные, то процесс называется непрерывным марковским процессом. Наиболее важным классом таких процессов является множество диффузионных процессов.