
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства функции корреляции
|
|
Рассмотрим основные свойства функции корреляции R x(t1, t2) случайного процесса x(t).
1. Функция корреляции является симметрической функцией своих аргументов
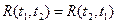 ,
,
что следует непосредственно из определения.
Для стационарных процессов функция корреляции – чётная функция
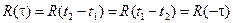 .
.
2. Для корреляционной функции выполняется неравенство
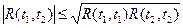 .
.
Для стационарных случайных процессов это неравенство означает, что в нуле функция корреляции достигает наибольшего значения.
3. Если для стационарного случайного процесса при t®¥ случайные величины x(t) и x(t+t) стохастически независимы, то
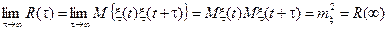 .
.
Тогда среднее значение процесса можно выразить через его функцию корреляции
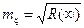 .
.
Далее, используя определение дисперсии процесса, запишем
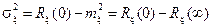 .
.
Таким образом, среднее значение и дисперсию стационарного случайного процесса можно найти, если известна его функция корреляции.
4. Функция корреляции случайного процесса является положительно определённой, то есть для " n произвольных действительных чисел l1, l2, …, ln, выполняется неравенство
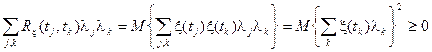 .
.
5. Корреляционная функция суммы случайных процессов равна сумме корреляционных функций слагаемых плюс сумма всех взаимных корреляционных функций этих слагаемых.
Это означает, что для 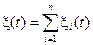
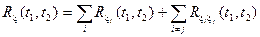 .
.
Для некоррелированных слагаемых с нулевыми средними значениями имеем

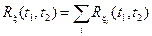 .
.
Для решения задач на практике можно использовать ряд свойств функции корреляции, доказательство которых следует из определения.
Пусть заданы неслучайные функция j(t) и y(t), случайные процессы x(t) и h(t) и их корреляционные функции Rx (t 1, t 2) Rh (t 1, t 2), ковариационные функции Kx (t 1, t 2), Kh (t 1, t 2), взаимная функция корреляции Rxh (t 1, t 2).
1. Если случайный процесс задан соотношением 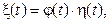 то
то
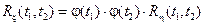 .
.
2. Если случайный процесс задан соотношением 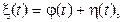 тогда
тогда
 .
.
3. Если случайный процесс задан соотношением  тогда
тогда
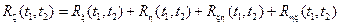 .
.
4. Если случайный процесс задан соотношением 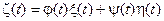 тогда
тогда
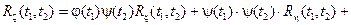
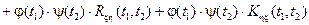 .
.
Пример 1.7. Пусть случайный процесс 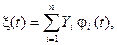 tÎ T, где Yi –некоррелированные случайные величины математическими ожиданиями mi и дисперсиями Di, а ji(t) – заданные на T детерминированные функции. Найти mx(t), Dx(t) и Rx(t, s).
tÎ T, где Yi –некоррелированные случайные величины математическими ожиданиями mi и дисперсиями Di, а ji(t) – заданные на T детерминированные функции. Найти mx(t), Dx(t) и Rx(t, s).
Решение. Согласно определениям имеем
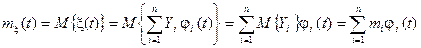 ,
,
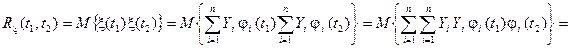
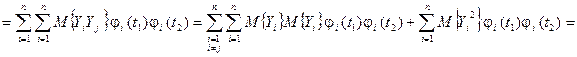
 ,
,
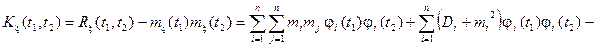
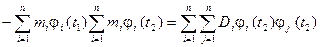 ,
,
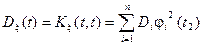 .
.
Наряду с корреляционной функцией для стационарных случайных процессов широко используется, так называемая, спектральная плотность S x(w), которая определяется следующим образом
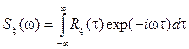
и иногда интерпретируется как средняя мощность гармонической составляющей частоты w электрического сигнала x(t).
Пример 1.8. Корреляционная функция случайного процесса 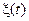 задана в виде
задана в виде 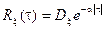 , где
, где 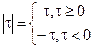 . Определить спектральную плотность соответствующего случайного процесса.
. Определить спектральную плотность соответствующего случайного процесса.
Решение. Спектральная плотность определяется по формуле:
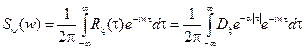 .
.
Исходя из условий задачи, представим этот интеграл в виде суммы двух интегралов:
 .
.
Вычислим
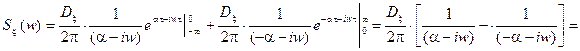
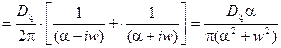 .
.