Эргодические теоремы для цепей Маркова

Теорема (основная эргодическая теорема). Рассмотрим неразложимую, непериодическую, возвратную цепь Маркова со счётным числом состояний, тогда имеет место равенство

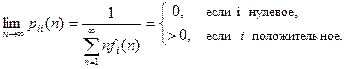
При этих же условиях .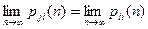

Теорема. Для неразложимой, непериодической, возвратной и положительной цепи Маркова со счётным числом состояний существуют пределы 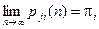, где 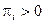и однозначно определяются условиями:

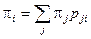–уравнение Колмогорова для финальных вероятностей,

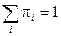–условием нормировки для финальных вероятностей.

Распределение вероятностей p _i называется финальным или эргодическим, а цепь Маркова называется эргодической.

Теорема (альтернативы). Пусть для марковской цепи со счётным числом состояний существуют пределы 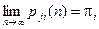, при этом выполняется равенство 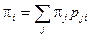, тогда возможна одна из двух альтернатив: все p _i= 0 или .

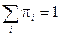Если 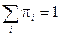, то набор вероятностей p _i образует единственное стационарное распределение вероятностей состояний цепи Маркова.

Если p _i= 0, то не существует стационарного распределения для рассматриваемой цепи Маркова.

Теорема (эргодическая теорема для цепей Маркова с конечным числом состояний). Для неразложимой непериодической цепи Маркова с конечным числом состояний существуют пределы

,

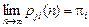не зависящие от j и удовлетворяющие условию нормировки.

Таким образом, если цепь Маркова неразложимая, непериодическая, возвратная и положительная, то для неё существует стационарное (финальное) распределение вероятностей.

Определение. Если для однородной цепи Маркова существуют финальные вероятности, то говорят, что для этой цепи существует стационарный режим функционирования.

Пример 2.6. Найти финальные вероятности для цепи Маркова заданной графом

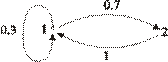
Решение: Данная цепь Маркова является неразложимой и апериодической, так как d (1)= d (2)=1. Кроме того, она имеет конечное число состояний, поэтому является эргодической.

Матрица вероятностей переходов .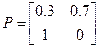

Составим систему уравнений для нахождения финальных вероятностей:

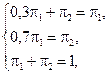
откуда находим p₁=10/17, p₂=7/17.