Финальные вероятности

Для однородной неразложимой цепи Маркова с конечным числом состояний существует предел 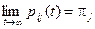, " j, не зависящий от i, который называется финальной вероятностью j -го состояния, а их совокупность – финальным распределением.

Финальные вероятности определяются из системы линейных алгебраических уравнений 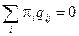, с учетом условия нормировки .

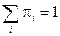Если ввести матричные обозначения 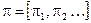, , 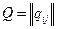, 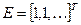то уравнения для нахождения финальных вероятностей можно записать в виде

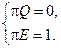
Если вероятности состояний не зависят от t, то есть P_j (t)º P_j, то P_j называются стационарными вероятностями, а их совокупность стационарным распределением.

Из прямой системы уравнений для стационарных вероятностей получим, что стационарное распределение определяется системой уравнений

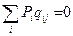
и условием нормировки

,

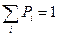совпадающими с системой уравнений для финальных вероятностей, следовательно, стационарное и финальное распределения совпадают.

Если для однородной цепи Маркова для системы дифференциальных уравнений в качестве начального распределения q_i (s) выбрать финальное p _i, то решение P_i (t) этой системы совпадает с финальным распределением, то есть для любых t³ s выполняется равенство

.

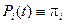В рассмотренном выше примере 3.1 финальные вероятности можно найти предельным переходом, устремив t® ¥:

, .
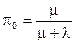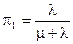