Время пребывания цепи Маркова в j-ом состоянии

Пусть величина t _j – остаточное время пребывания цепи Маркова в j -ом состоянии. Обозначим её закон распределения B_j (x)= P {t _j ³ x }, тогда, используя марковское свойство цепи, можно записать равенство

,

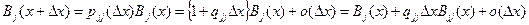выполнив в котором несложные преобразования, получим уравнение

,

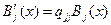определяющее вид функции B_j (x).

Из полученного дифференциального уравнения следует, что

,

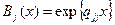следовательно, величина t _j имеет экспоненциальное распределение с параметром – q_jj. В силу свойства отсутствия последействия экспоненциального распределения, полное (не остаточное) время пребывания цепи Маркова в j -ом состоянии также имеет экспоненциальное распределение с тем же параметром – q_jj. Среднее значение этого времени составляет –1/ q_jj.

Таким образом, равенство для финальных вероятностей можно переписать в виде

,

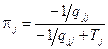следовательно, финальная (стационарная) вероятность p_j равна отношению среднего значения времени пребывания цепи Маркова в j -ом состоянии к сумме этого значения и среднего значения T_j – времени возвращения в это состояние, то есть вероятность p_j имеет смысл доли времени проведённого цепью в состоянии j.