Простейший поток

Случайным потоком однородных событий называется последовательность t ₁< t ₂< …< t_n моментов наступления событий. Обозначим m (t) – число событий наступивших за время t. Пусть для этого процесса выполнены следующие условия.

Стационарность. Поток называется стационарным, если число событий, наступивших на интервале [ s, t), не зависит от положения этого интервала на оси времени, а определяется лишь его длиной t–s.

Последействие. Число событий, наступивших на некотором интервале времени не зависит от числа событий, наступивших на других, не пересекающихся с ним, интервалах.

Ординарность. Вероятность наступления более одного события за бесконечно малый промежуток времени является бесконечно малой более высокого порядка, чем длина рассматриваемого промежутка.

Обозначим через p_k (D t) вероятность того, что на интервале D t наступит k событий. Эти вероятности определяются равенствами

,

,

, .

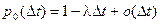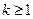Определение. Случайный поток однородных событий, удовлетворяющий всем трем свойствам, называется простейшим.

Величина l называется параметром или интенсивностью потока.

Простейший поток имеет важное значение по причине того, что существует возможность доказать, что при взаимном наложении (суперпозиции) большого количества потоков с последствием, возникает суммарный поток, который можно охарактеризовать как простейший, и тем точнее, чем большее число потоков суммируется. В качестве дополнительного условия важно, чтобы суммируемые потоки предполагали соответствие по интенсивности, иными словами необходимо, чтобы среди потоков не существовало одного, который по показателю интенсивности превосходил бы сумму всех остальных.

Впервые описание модели простейшего потока появились в работах выдающихся физиков начала века – А. Эйнштейна и Ю.Смолуховского, посвященных броуновскому движению.

Пример 3.4. Найти распределение вероятностей числа наступивших событий в простейшем потоке.

Решение: Рассмотрим процесс m (t) – число наступивших событий простейшего потока за время t. Для вероятностей получим систему дифференциальных уравнений Колмогорова.

Учитывая отсутствие последствия, можно записать

.

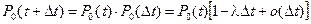Аналогично, для можно записать

.

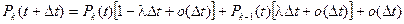После предельного перехода 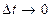, получаем систему дифференциальных уравнений вида

,

.

Для однозначного решения этой системы надо добавить граничное условие, которое естественно брать в виде

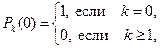
так как в силу ординарности потока на интервале нулевой длины с вероятностью 1 не будет ни одного события

Метод производящих функций

Для решения этой системы дифференциально-разностных уравнений воспользуемся методом производящих функций, обозначив

,

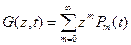систему уравнений Колмогорова перепишем в виде уравнения

,

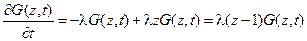с начальным условием

.

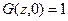Это уравнение легко решается методом разделения переменных

,

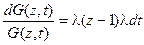откуда, интегрируя в пределах (0, t), получим

.

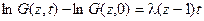Но, как следует из граничного условия,

,

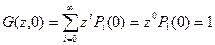и поэтому

,

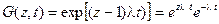Разлагая 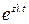в ряд Тейлора, запишем

,

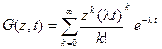откуда получаем формулу для распределения вероятностей числа событий простейшего потока

.

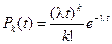Очевидно, что число событий, наступивших за произвольный фиксированный интервал времени, распределено по закону Пуассона.