
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава 5. Непрерывные марковские процессы
|
|
Рассмотрим ещё один класс марковских процессов, который характеризуется тем, что не только время, но и множество состояний этих процессов непрерывно. Такие процессы образуют класс непрерывных марковских процессов, являющихся достаточно адекватными моделями многих реальных процессов.
Случайный процесс x(t) называется непрерывным марковским, если для любых моментов времени s ׳ < s < t Î T и любых действительных y выполнено равенство
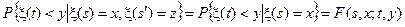 .
.
Условная функция распределения F (s, x; t, y) называется марковской переходной функцией.
Задание этой функции и начального распределения вероятностей состояний полностью определяет марковский процесс. Если существует производная
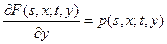 ,
,
которая называется плотностью вероятностей переходов, то для марковской переходной функции можно записать
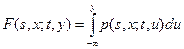 .
.
Очевидно, что марковская переходная функция удовлетворяет следующим условиям:
1) для любых s, x, t марковская переходная функция по y является функцией распределения, то есть
 ,
,
 ,
,
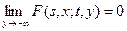 ;
;
2) для любых s< u< t марковская переходная функция удовлетворяет уравнению Чепмена-Колмогорова
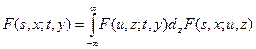 ,
,
или
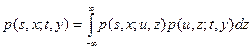 ;
;
3) марковская переходная функция удовлетворяет условию стохастической непрерывности
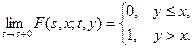
Это условие требует, чтобы при достаточно малом времени функционирования процесса его вероятностная мера была сосредоточена около точки, из которой стартует процесс.
Если марковская переходная функция по времени зависит только от разности моментов времени t–s, то процесс называется однородным марковским процессом
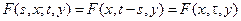 .
.
Для однородного марковского процесса уравнение Чепмена-Колмогорова примет вид
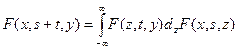
или для плотности вероятностей переходов
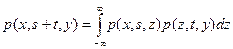 .
.