Система массового обслуживания, основные определения и классификация

Под системой массового обслуживания (СМО) понимают динамическую систему, предназначенную для эффективного обслуживания потока заявок (требований на обслуживание) при ограничениях на ресурсы системы.

Определение. Система массового обслуживания – это такие система, в которой в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжение системы каналов обслуживания (рис.9).

Рис.9. Общая схема системы массового обслуживания.

На вход СМО поступают заявки на обслуживание, образующие входящий поток.

Первопричину заявок, какова бы ни была её физическая природа, называют источником заявок.

В зависимости от характера источника заявок различают разомкнутые и замкнутые СМО. В разомкнутых СМО число заявок, вырабатываемых источником, считается неограниченным, поведение источника заявок не связано с состоянием СМО ни в данный, ни в какой-либо из предшествующих моментов времени. Для замкнутых СМО характерно конечное числу заявок, циркулирующих в системе источник – СМО. Обслуженные заявки возвращаются в источник и через некоторое, в общем случае, время могут вновь появиться на входе СМО. Поведение источника в замкнутых СМО является некоторой функцией состояния СМО.

Различают “терпеливые” заявки, т.е. такие, на время пребывания которых в СМО не накладывается никаких ограничений, и “нетерпеливые”, способные уйти из системы, не будучи обслуженными, если время пребывания их в СМО превысит допустимую величину.

Параметры структуры СМО. Каждая система массового обслуживания обладает определённой структурой, характеризующейся совокупностью параметров. Основным компонентом структуры СМО являются каналы обслуживания. В зависимости от числа каналов различают одноканальные и многоканальные СМО. В свою очередь, многоканальные СМО могут содержать одинаковые и различные по производительности каналы обслуживания.

Производительность канала обслуживания обратна длительности обслуживания заявки, равной промежутку времени, необходимому каналу обслуживания для обслуживания заявки. В общем случае это случайная величина с функцией распределения, плотностью распределения и математическим ожиданием T _об. Типы заявок различаются либо законами распределения, либо только математическими ожиданиями при одинаковых законах распределения. При этом принимается допущение о независимости длительностей обслуживания для различных заявок одного типа, вполне корректное для большинства реальных систем. Наряду с математическим ожиданием длительности обслуживания используется понятие интенсивности потока обслуживания m=1/ T _об – величины, обратной средней длительности обслуживания и характеризующей количество заявок, которое может быть обслужено в единицу времени постоянно загруженным каналом обслуживания. Наибольшее число результатов получено для длительности обслуживания с экспоненциальной плотностью распределения

.

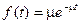Если в момент появления заявки на входе СМО хотя бы один канал свободен от обслуживания, её обслуживание может быть начато немедленно, без задержки. Однако вполне вероятна ситуация, когда заявка застает СМО полностью загруженной, то есть когда все m каналов обслуживания заняты обслуживанием. В этом случае начало обслуживания задерживается, заявка может занять место в соответствующей очереди. Таким образом, вторым важным компонентом структуры СМО является очередь, параметром которой является число мест в очереди n. В приоритетных системах общая очередь может быть разделена на несколько очередей по числу различаемых системой приоритетов, для каждой из которых должно быть указано число мест n_i i =1, 2, …, N. На число мест в очереди может быть наложено ограничение, это может быть сделано как для каждой очереди в отдельности, так и для всей совокупности очередей в целом. При этом возможны конфликтные ситуации, решением которых может быть отказ системы принять заявку.

В зависимости от числа мест в очереди различают СМО с отказами и, соответственно, СМО без отказов. В СМО с отказами число мест в очереди конечно, и вследствие вероятного характера как входящего потока, так и процессов обслуживания, существует ненулевая вероятность того, что поступившая на вход СМО заявка застанет все каналы занятыми обслуживанием и все места в очереди занятыми ожидающими обслуживания заявками, то есть она получит отказ. В СМО без отказов заявка либо сразу назначается на обслуживание, если в момент ее поступления свободен хотя бы один канал обслуживания, либо безусловно принимается в очередь на обслуживание.

Для описания СМО используется символика Кендалла в виде

A | B | N₁ | N₂ | f.

Здесь первый символ означает входящий поток заявок. Наиболее часто встречаются следующие символы:

М – простейший поток заявок с постоянной интенсивностью;

М (t) – пуассоновский с ;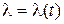

E_k – эрланговский поток k -го порядка;

G_I – рекуррентный поток;

G – поток с зависимыми интервалами.

Если потоков n, то индексом указывается число потоков и вверху ставится стрелка; например, 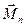означает, что в систему поступает n простейших потоков заявок постоянной интенсивности.

Второй символ – распределение времени обслуживания:

M – экспоненциальное распределение;

E_k – эрланговское порядка k;

G – распределение времени обслуживания произвольное.

Если время обслуживания разное для разных типов заявок, то над соответствующим символом ставится стрелка.

N ₁ – число обслуживающих приборов;

N ₂ – число мест для ожидания.

Что касается дисциплины обслуживания, то мы рассмотрим лишь те дисциплины, которые встречаются в СМО с одним входящим потоком. Наиболее часто используются:

FIFO – «first input – first output» – дисциплина «первым пришел – первым обслужен»;

LIFO – «last input – first output» – дисциплина «последний пришел – первый обслужен».

Систему массового обслуживания будем называть марковской, если процесс изменения ее состояний является цепью Маркова с непрерывным временем. Удобным способом задания марковских СМО являются графы вероятностей переходов состояний таких систем. Для марковских СМО графы вероятностей переходов строятся совершенно аналогично построению таких графов для цепей Маркова с непрерывным временем.

Вершина графа обозначает состояние системы. Ребра графа ориентированы и показывают возможные переходы из одного состояния в другое. В графе рисуют лишь те ребра, которые показывают переходы с ненулевыми инфинитезимальными характеристиками. Эти характеристики обычно пишут рядом с ребрами и называют весами ребер.

Приведем несколько примеров таких графов для простейших марковских СМО и соответствующих систем дифференциальных уравнений, определяющих распределение вероятностей состояний этих систем.

Система M/M/1/¥ (с очередью)

Рассматриваемая СМО состоит из одного обслуживающего прибора (одной линии), на который поступает простейший поток заявок (требований) с интенсивностью l. Если в системе нет заявок, то поступившая заявка занимает прибор для своего обслуживания, продолжительность которого случайная, распределенная по экспоненциальному закону с параметром m. Если в момент поступления заявки прибор занят, то поступившая заявка становится в очередь (поступает в бункер). Считается, что длина очереди (объем бункера) может быть сколь угодно велика. В момент освобождения прибора из очереди по какому-то правилу выбирается следующая заявка для обслуживания.

Пусть i (t) есть число заявок, находящихся в системе в момент времени t. В силу свойств простейшего потока и экспоненциального обслуживания, процесс i (t) является цепью Маркова с непрерывным временем. Граф вероятностей переходов для процесса i (t) изображен на рис.10.

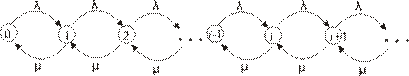
Рис. 10.

Обозначим P_i (t)= P { i (t)= i }. Так как

,

,

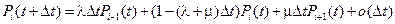то, выполнив несложные преобразования, получим систему дифференциальных уравнений

,

, ,

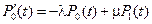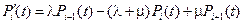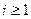определяющую распределение вероятностей P_i (t) числа заявок в рассматриваемой СМО.

Осуществив предельный переход t®¥, получим систему

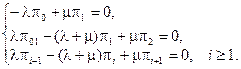
Из первого уравнения имеем 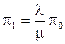, из второго 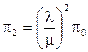, аналогично .

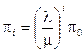При решении систем уравнений, определяющих финальные вероятности, следует иметь в виду, что одна из констант всегда остается неопределенной; она находится из условия нормировки 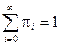. Это условие нормировки следует всегда добавлять к системе уравнений, определяющих финальные вероятности.

В нашем случае условие нормировки имеет вид

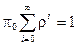, где .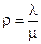

Так как входящий сюда ряд сходится при r< 1, то и стационарный режим существует лишь при r< 1. В этом случае и .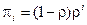

Финальные вероятности позволяют найти ряд важных характеристик СМО.

Среднее число заявок в системе

.

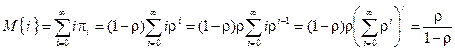Средняя длина очереди

Так как длина очереди равна i– 1 и очередь есть лишь при i> 1, то

.

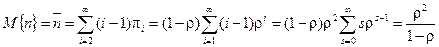Дисперсия числа заявок

.

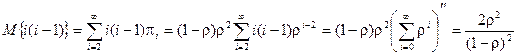Отсюда

.
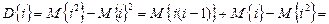
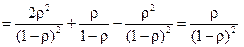