Определение диффузионного случайного процесса

Среди непрерывных марковских процессов наиболее важную роль играют, так называемые, диффузионные случайные процессы. Это название оправдано тем, что процессы этого класса являются достаточно адекватными математическими моделями движения частиц в процессах диффузии. Кроме того, они могут быть использованы как предельные модели для случайных процессов с дискретным множеством состояний, описывающих явления в биологии, социологии, демографии, теории массового обслуживания.

Определение. Непрерывный марковский процесс называется диффузионным, если его марковская переходная функция удовлетворяет следующим условиям.

1. Для " e> 0 и любых x равномерно по s< t выполняется предельное равенство

.

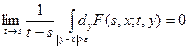Это условие требует, чтобы вероятность того, что |x(t)–x(s)|> e, была бы величиной бесконечно малой бале высокого порядка малости, чем | t – s |, при t ® s.

2. Существуют функции a (s, x) и b (s, x) такие, что

,

,

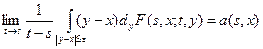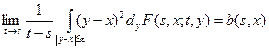здесь функция a (s, x) называется коэффициентом переноса, а функция b (s, x) – коэффициентом диффузии.

3. Для любых k > 2

.

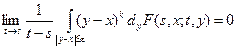Для однородных диффузионных процессов коэффициенты переноса и диффузии не зависят от времени s, то есть имеют вид

.

При выполнении некоторых ограничений эти коэффициенты полностью определяют рассматриваемый диффузионный процесс. Сформулируем эти ограничения ври выводе прямого и обратного уравнений Колмогорова.