Обратное уравнение Колмогорова

Теорема. Пусть 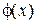– ограниченная функция такая, что

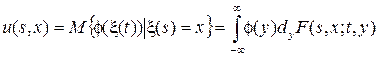
имеет ограниченные непрерывные производные по x первого и второго порядка, а коэффициенты переноса a (s, x) и диффузии b (s, x) являются непрерывными функциями своих аргументов. Тогда u (s, x) дифференцируема по s и удовлетворяет уравнению

,

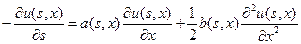а также краевому условию

.

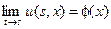Следствие. Марковская переходная функция F (s, x; t, y) удовлетворяет уравнению

,

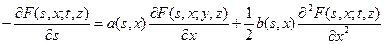которое называется обратным уравнением Колмогорова.

Если существует переходная плотность

,

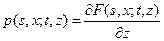то она также удовлетворяет обратному уравнению Колмогорова

.

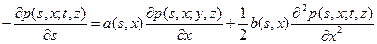Решение этих уравнений достаточно полно определяет функционирование диффузионных процессов. Для нахождения их однозначных решений необходимо задать краевые условия, определяемые условием стохастической непрерывности в виде

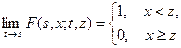
для марковской переходной функции, или в виде

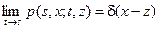
для переходной плотности распределения.

Прямое уравнение Колмогорова. Уравнение Фоккера-Планка

Теперь получим прямое уравнение Колмогорова, которое является сопряжённым к обратному и ещё называется уравнением Фоккера-Планка. Для вывода этого уравнения необходимо существование переходной плотности распределения, так как прямое уравнение составлено именно для переходной плотности распределения p (s, x; t, y).

Теорема. Если для переходной плотности распределения p (s, x; t, y) существуют производная по t, а также первая и вторая производные по y, то для любых y и всех t > s переходная плотность распределения p (s, x; t, y) удовлетворяет уравнению

,

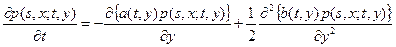которое называется прямым уравнением Колмогорова или уравнением Фоккера-Планка.

Некоторые частные случаи уравнения Фоккера-Планка

Рассмотрим некоторые частные случаи уравнения Фоккера-Планка.

1. Для однородного диффузионного процесса

,

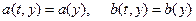а переходная плотность распределения вероятностей p (s, x; t, y) зависит лишь от разности моментов времени, то есть имеет вид

,

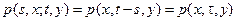поэтому уравнение Фоккера-Планка примет вид

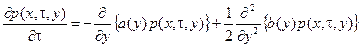
с начальным условием .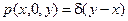

Если при t®¥ существует предел

,

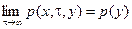не зависящий от x, то функцию p (y) называют финальной или стационарной плотностью распределения вероятностей значений однородного диффузионного процесса.

Для стационарной плотности распределения уравнение Фоккера-Планка примет вид

,

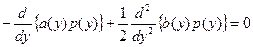который получается если положить p (t, y)º p (y). Решение этого уравнения не представляет труда, так как оно относится к классу обыкновенных линейных дифференциальных уравнений первого порядка

,

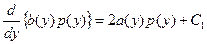где C ₁ – произвольная постоянная, полученная в результате интегрирования исходного уравнения.

2. Рассмотрим диффузионный процесс авторегрессии, для которого коэффициенты переноса и диффузии имеют вид a (y)=-a y, b (y)=s², тогда уравнение предыдущее уравнение при C ₁=0 перепишем следующим образом

.

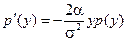Его решение, удовлетворяющее условию нормировки, запишем в виде

,

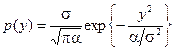то есть решением p (y) этого уравнения является плотность нормального распределения с нулевым математическим ожиданием и дисперсией равной .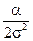

3. Винеровским диффузионным процессом будем называть однородный диффузионный процесс с коэффициентами переноса и диффузии вида a (y)=0 b (y)=s², тогда уравнение Фоккера-Планка примет вид

.

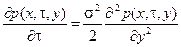Решение этого уравнения выполним методом характеристических функций

.

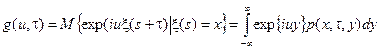Домножив левую и правую части этого уравнения на e^iuy и проинтегрировав их по yÎ (– ¥, ¥), получим равенство

.

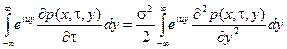Здесь

,

.

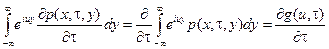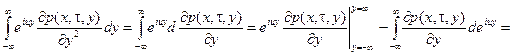
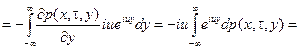
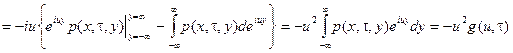Поэтому можно записать

,

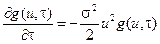то есть в виде обыкновенного линейного дифференциального уравнения первого порядка, решение которого, удовлетворяющее начальному условию

,

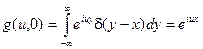имеет вид

,

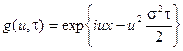то есть вид характеристической функции нормального распределения с математическим ожиданием равным x и дисперсией равной s²t, следовательно, переходная плотность распределения вероятностей p (x, t, y) имеет вид

.
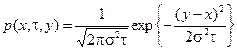