Связь интегралов Ито и Стратановича

Рассмотрим связь стохастических интегралов в форме Ито и в форме Стратановича.

Пусть подынтегральная функция F(x, t) дифференцируема по первому аргументу. Тогда, разлагая её в ряд Тейлора в окрестности точки x(t_i), получим

.

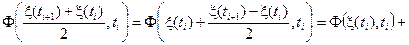
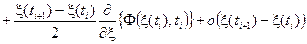Подставляя это разложение (6.2), получим

.

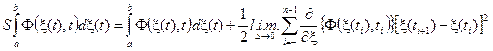В силу замечания о произвольном диффузионном процессе из предыдущей главы, последнее равенство можно переписать в виде

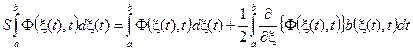. (6.3)

Для стохастических интегралов, определённых по винеровскому процессу, это равенство запишем в виде

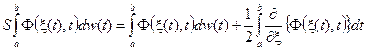. (6.4)

Рассмотрим стохастический интеграл в форме Стратановича

.

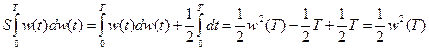То есть результаты интегрирования по Стратановичу совпадают с результатами интегрирования по Риману.

Из равенств (6.3) и (6.4) следует, что если подынтегральная функция F(x, t) не зависит от x, то интегралы в форме Ито и Стратановича совпадают.

При рассмотрении прикладных задач обычно применяют интеграл Стратановича, а в теоретических исследованиях применяют интеграл Ито, затем, используя равенства (6.3) и (6.4) вновь возвращаются к интегралам в симметризованном виде.

Применение интегралов Ито в теоретических исследованиях оправдано его некоторыми полезными свойствами, которые более подробно будут рассмотрены в следующей главе.