Формула дифференцирования Ито

Пусть x(t) – диффузионный процесс с коэффициентами переноса a (x, t) и диффузии s²(x, t), тогда этот процесс является решением стохастического дифференциального уравнения (7.2)

.

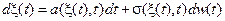Пусть f (x, t) – непрерывная детерминированная функция такая, что для неё существуют непрерывные производные

.

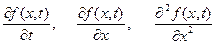Рассмотрим случайный процесс

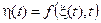. (7.6)

Ито показал, что этот случайный процесс является диффузионным. Найдём дифференциал этого диффузионного процесса

,

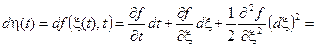
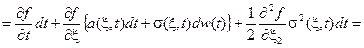
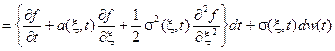то есть

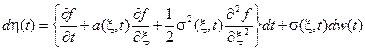. (7.7)

Из равенства (7.6) процесс x(t) выразим через h(t) и t и это выражение подставим в (7.7), получим коэффициенты переноса и диффузии для диффузионного случайного процесса h(t), а равенство (7.7) запишем в виде

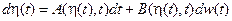, (7.8)

где функци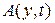и и 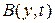имеют вид выражений

,

,

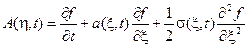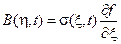в которых x в силу равенства (7.6) выражена через h и t.

Равенства (7.7) и (7.8) будем называть формулами дифференцирования Ито.

Формулы дифференцирования Ито находят широкое применение для решения стохастических дифференциальных уравнений.