
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение стохастических дифференциальных уравнений
|
|
Решение стохастических дифференциальных уравнений проиллюстрируем следующими примерами.
Пример 7.1. Процесс x(t) арифметического броуновского движения определяется начальным условием x(0)=x0 и стохастическим дифференциальным уравнением
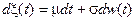 ,
,
Решение. Применяя определение (7.3), получим
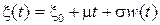 .
.
Пример 7.2. Процесс геометрического броуновского движения аналогично определяется начальным условием x(0)=x 0 и стохастическим дифференциальным уравнением
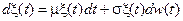 .
.
Решение. Рассмотрим процесс
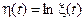 , (7.9)
, (7.9)
применяя к которому формулу дифференцирования Ито, получим
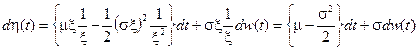 ,
,
то есть h(t) является процессом арифметического броуновского движения, поэтому в силу примера 7.1 его можно записать в виде
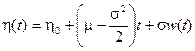 ,
,
тогда в силу замены (7.9) процесс x(t) представим в виде
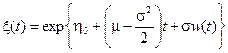 .
.
Так как, 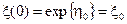 , то окончательно запишем
, то окончательно запишем
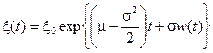 .
.
Пример 7.3. Для диффузионного процесса авторегрессии
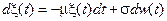 .
.
Решение. В этом уравнении выполним замену
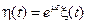 . (7.10)
. (7.10)
Применяя формулу дифференцирования Ито, получим
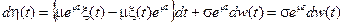 ,
,
следовательно
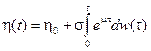 ,
,
поэтому в силу замены (7.10) можно записать
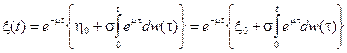 .
.
Пример 7.4. Для процесса броуновского моста
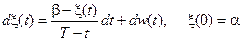 .
.
Решение. В этом уравнении выполним замену
 . (7.11)
. (7.11)
Применяя формулу дифференцирования Ито, получим
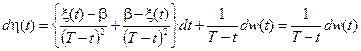 ,
,
следовательно
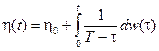 ,
,
поэтому в силу замены (7.11) можно записать
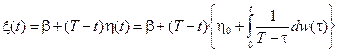 . (7.12)
. (7.12)
Здесь
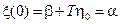 ,
,
следовательно
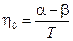 ,
,
поэтому в силу (7.12) можно записать
 .
.
Найдём математическое ожидание и дисперсию этого процесса
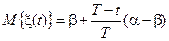 ,
,
в частности, получим
 , (7.13)
, (7.13)
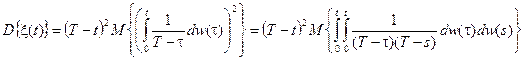 .
.
Так как приращения винеровского процесса на непересекающихся интервалах независимы, их математические ожидание равны нулю, а дисперсии равны длинам этих интервалов, то
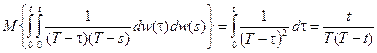 ,
,
поэтому
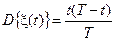 ,
,
и, в частности,
 . (7.14)
. (7.14)
В силу равенств (7.14) и (7.13) можно говорить, что броуновский мост соединяет в среднем квадратическом точки 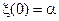 и
и 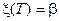 , что оправдывает название этого диффузионного случайного процесса.
, что оправдывает название этого диффузионного случайного процесса.
Литература
1. Баруча-Рид А.Т. Элементы теории марковских процессов и их приложения. – М.: Изд-во «Наука», 1969. – 512 с.
2. Волков И.К., Зуев С.М., Цветкова Г.М. Случайные процессы: Учеб. для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 1999.– 448 с.
3. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. Изд. 3-е, испр. и доп. – М.: КомКнига, 2005. – 400 с.
4. Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1969. – 448 с.
5. Маталыцкий М.А. Элементы теории случайных процессов: Учеб. пособие. – Гродно: ГрГУ, 2004. – 326 с.
6. Миллер Б.М., Панков А.Р. Теория случайных процессов в примерах и задачах. – М.: ФИЗМАТЛИТ, 2002. – 320 с.
7. Назаров А.А., Терпугов А. Ф. Теория вероятностей и случайных процессов: учеб. пособие. – Томск: Изд-во НТЛ, 2006. – 204 с.
8. Назаров А.А., Терпугов А.Ф. Теория массового обслуживания: Учебное пособие. – Томск: Изд-во НТЛ, 2004.
9. Саати Т.Л. Элементы теории массового обслуживания и ее приложения. – М.: Сов. Радио, 1971.
Содержание
Введение. 1
Глава 1. Элементы теории случайных процессов. 2
Определение и описание случайного процесса. 2
Задачи для самостоятельного решения. 5
Статистические средние характеристики случайных процессов. 8
Стационарные случайные процессы.. 10
Свойства функции корреляции. 11
Эргодические случайные процессы.. 14
Задачи для самостоятельного решения. 16
Глава 2. Цепи Маркова с дискретным временем.. 21
Основные определения. 21
Цепи Маркова с дискретным временем.. 22
Классификация состояний цепи Маркова с дискретным временем.. 26
Структура периодического замкнутого класса. 29
Классификация состояний цепи Маркова по асимптотическим свойствам переходных вероятностей 30
Эргодические теоремы для цепей Маркова. 31
Вероятностно-временные характеристики цепи Маркова. 33
Задачи для самостоятельного решения. 38
Глава 3. Цепи Маркова с непрерывным временем.. 46
Дифференциальные уравнения Колмогорова. 48
Финальные вероятности. 51
Время перехода из одного состояния в другое. 52
Статистический смысл финальных (стационарных) вероятностей. 53
Время пребывания цепи Маркова в j -ом состоянии. 53
Процессы гибели и размножения. 55
Процесс чистого размножения. 57
Простейший поток. 57
Основные вероятностные характеристики простейшего потока. 60
Задачи для самостоятельного решения. 64
Глава 4. Элементы теории массового обслуживания. 70
Система массового обслуживания, основные определения и классификация. 70
Система M/M/1/¥ (с очередью) 74
Система M/M/N.. 75
Задачи для самостоятельного решения. 77
Глава 5. Непрерывные марковские процессы.. 83
Определение диффузионного случайного процесса. 84
Обратное уравнение Колмогорова. 85
Прямое уравнение Колмогорова. Уравнение Фоккера-Планка. 86
Некоторые частные случаи уравнения Фоккера-Планка. 86
Допредельная модель диффузионного процесса. 89
Глава 6. Стохастические интегралы.. 91
Стохастический интеграл в форме Ито. 91
Особенность стохастического интеграла в форме Ито. 91
Стохастический интеграл в форме Стратановича. 92
Связь интегралов Ито и Стратановича. 93
Глава 7. Стохастические дифференциальные уравнения. 94
Определение стохастических дифференциальных уравнений. Свойства их решений. 94
Формула дифференцирования Ито. 96
Решение стохастических дифференциальных уравнений. 97
Литература. 101
Содержание. 102