Определение стохастических дифференциальных уравнений. Свойства их решений

Многие реальные процессы определяются дифференциальными уравнениями вида

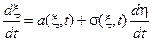
или в форме дифференциалов

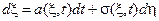. (7.1)

Если h(t)= w (t) – винеровский процесс, то уравнение (7.1) называется стохастическим дифференциальным уравнением. В этом случай уравнение (7.1) будем записывать в виде

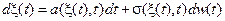. (7.2)

В силу недифференцируемости винеровского процесса, необходимо определить в каком смысле следует понимать уравнение (7.2).Это равенство будем понимать как форму записи интегрального уравнения

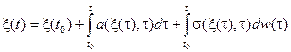, (7.3)

где первый интеграл является интегралом в среднем квадратическом, а второй – стохастическим интегралом в форме Ито.

Покажем, что решение x(t) стохастического дифференциального уравнения (7.2) является диффузионным случайным процессом.

Действительно, из (7.3) следует, что распределение вероятностей значений сечения x(t) при t> t ₀ зависит лишь от значения x(t ₀) и не зависит от значений рассматриваемого процесса для моментов времени s> t ₀, следовательно, процесс x(t) марковский.

Дифференциальное уравнение(7.2) запишем в конечных разностях

.

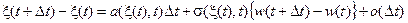Важно заметить, что случайные величины x(t) и D w (t)= w (t +D t)– w (t) стохастически независимы.

Проверим для процесса x(t) выполнение свойств диффузионного процесса.

Очевидно, что условное распределение приращения Dx(t)=x(t +D t)–x(t), при условии, что x(t)= x является гауссовским с математическим ожиданием и дисперсией вида

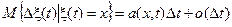, (7.4)

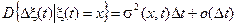. (7.5)

Далее покажем, что

,

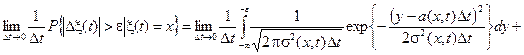
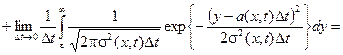
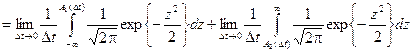где

.

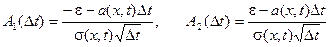Нетрудно показать, что рассматриваемые пределы равны нулю. Выполнение остальных свойств, очевидно, следует из равенств (7.4) и (7.5).

Таким образом, решение x(t) стохастического дифференциального уравнения (7.2) является диффузионным случайным процессом с коэффициентом переноса – a (x, t), и коэффициентом диффузии – b (x, t)=s²(x, t). Очевидно, что эти коэффициенты диффузионного процесса однозначно определяются коэффициентами стохастического дифференциального уравнения.

Знание коэффициентов переноса и диффузии позволяет записать уравнение Фоккера-Планка для переходной плотности распределения вероятностей, которая однозначно определяет функционирование диффузионного случайного процесса x(t).

Приведём примеры наиболее часто применяемых стохастических дифференциальных уравнений.

1) Арифметическое броуновское движение

.

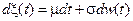2) Геометрическое броуновское движение. Модель Самуэльсона

.

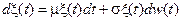3) Диффузионный процесс авторегрессии

.

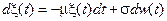4) Процесс, возвращающийся к среднему как квадратный корень (Mean Reverting Square Root, MRSR-процесс)

.

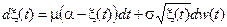5) Процесс Орнштейна-Уленбека

.

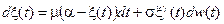6) Броуновский мост

.
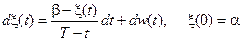