
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Система M/M/N
|
|
Рассмотрим N -линейную СМО, на вход которой поступает простейший с параметром l поток заявок. Обслуживание каждым прибором экспоненциальное с параметром μ. Необходимо найти стационарное распределение p(i) числа занятых приборов, если заявки, поступившие в систему, когда заняты все приборы, теряются.
Пусть i (t) есть число заявок, находящихся в системе в момент времени t. В силу свойств простейшего потока и экспоненциального обслуживания, процесс i (t) является цепью Маркова с непрерывным временем. Граф вероятностей переходов для процесса  изображен на рис.11.
изображен на рис.11.

Рис. 11.
Очевидно, финальные вероятности p(i) удовлетворяют системе уравнений
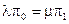 ,
,
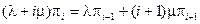 ,
,
 ,
,
из которой нетрудно получить рекуррентные соотношения
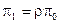 ,
,
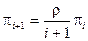 ,
,
 ,
,
откуда следует c учетом условия нормировки, что p i имеют вид
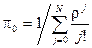 ,
,
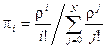 ,
,
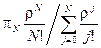 .
.
Заметим, что при 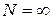 (бесконечнолинейная СМО) эти формулы принимают очень простой вид
(бесконечнолинейная СМО) эти формулы принимают очень простой вид
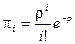 .
.
Полученные формулы называются формулами Эрланга и получены в 1921 году. В то же время Эрланг ставил задачу и пытался найти аналогичное распределение вероятностей, если обслуживание неэкспоненциальное. Эту задачу решил Севастьянов Б.А., опубликовав ее в работе «Эргодическая теорема для марковских процессов и ее применение к телефонным линиям» в журнале «Теория вероятностей и ее применение» еще в 1957г.
В теории телетрафика этими формулами пользуются до сих пор, хотя в связи с повышенной компьютеризацией и передачей по телефонным каналам разнородной информации требуется дальнейшее обобщение этих классических результатов.
Задачи для самостоятельного решения
1. В населенном пункте ведет прием один врач-инфекционист. Известно, что за бесконечно малый отрезок времени D t каждый больной с вероятностью l передает инфекцию здоровому человеку. Предположим, что после обращения к врачу больной становится не опасен для окружающих. Время лечения будем считать экспоненциальным с параметром m. Найти нестационарное распределение вероятностей числа больных. В начальный момент болен был один человек.
2. Имеется станция с тремя каналами связи. Среднее время обслуживания одной заявки каналом равно 2 минуты. Поток заявок простейший с интенсивностью l=1, 5 заявки в минуту. Составить граф состояний. Найти финальные вероятности состояний и основные характеристики эффективности СМО.
3. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается и предприятие вынуждено обратится в другой ВЦ. Среднее время работы с одним заказом составляет 3 часа. Интенсивность потока заявок 0, 25 заявок в час. Составить граф состояний. Найти вероятность отказа и среднее число занятых ЭВМ.
4. На АТС работает аппаратура, состоящая из 5 каналов. Считая, что l=3 и m=2, определить:
а) характеристики СМО при работе с отказами без очереди;
б) минимально необходимое число каналов для Pобсл= 0, 7.
5. Железнодорожная касса имеет два окошечка, в каждом из которых продаются билеты в два направления: на запад и на восток. Потоки пассажиров приобретающих билеты на запад и на восток одинаковы по интенсивности, которая равна 0, 45 пассажиров в минуту. Среднее время обслуживания пассажиров 2 минуты. Поступило рационализаторское предложение. Для уменьшения очередей необходимо сделать обе кассы специализированными: в первой продавать билеты только на запад, а во второй – только на восток. Считая, что все потоки простейшие, проверить разумность этого предложения.
6. Известно, что заявки на телефонные переговоры на переговорном пункте поступают с интенсивностью λ =90 заявок в час, а средняя продолжительность переговоров по телефону составляет 2 минуты. Определить показатели эффективности работы СМО при наличии одного телефонного аппарата.
7. Одноканальная СМО с отказами представляет собой одну телефонную линию, на вход которой поступает простейший поток вызовов с интенсивностью λ =0, 4 вызовов в минуту. Средняя продолжительность разговора 3 минуты; время разговора имеет экспоненциальное распределение. Найти финальные вероятности состояний СМО: p0 и p1.
8. В больнице есть 3 лифта. Среднее время занятости лифта 4 минуты. В среднем приходит 2 врача в минуту. Если лифт занят, то врач поднимается пешком. Найти вероятность того, что пришедший врач пойдет пешком.
9. Автоматическая телефонная станция имеет четыре линии связи. На станцию поступает простейший поток заявок с плотностью l=3 вызова в минуту. Вызов, поступивший в момент, когда все линии заняты, получает отказ. Средняя длительность разговора 2 минуты. Найти: а) вероятность отказа; б) среднюю долю времени, в течении которого телефонная станция вообще не загружена.
10. Поток желающих оформить вызов врача на дом – простейший. В среднем абоненты звонят через каждые 10 секунд. Время приема вызова распределено по показательному закону со средним значением 12 секунд. Определить наименьшее число телефонов в регистратуре, при котором вызов принимается не менее чем от 90% абонентов. Считается, что в случае неудачи абонент не предпринимает больше попыток дозвониться.
11. Интенсивность поступления требований на радиостанции 2 заявки в минуту при среднем времени на переговоры 2 минуты. Определить оптимальное число телефонных номеров на радиостанции, если условием оптимальности считать удовлетворение в среднем из каждых 100 заявок не менее 80 заявок на переговоры.
12. Автозаправочная станция имеет 4 бензоколонки. Среднее время заправки автомашины 2 минуты. Входящий поток автомашин – простейший с интенсивностью 1, 5 автомашины в минуту. При всех занятых колонках требование теряется. Определить вероятность отказа и среднее число занятых колонок.
13. АТС имеет 4 линии связи. На АТС поступает простейший поток с плотностью l=5 вызовов в минуту. Если все линии заняты, то вызов получает отказ. Средняя длительность разговора 2 минуты. Найти вероятность отказа.
14. Автоматическая телефонная станция имеет 4 линии связи. На станцию поступает простейший поток заявок с плотностью λ =3 вызова в минуту. Вызов, поступивший в момент, когда все линии заняты, получает отказ. Средняя длительность разговора 2 минуты. Найти: а) вероятность отказа; б) среднюю долю времени, в течение которой телефонная станция вообще не загружена.
15. Станция наведения истребителей имеет 3 канала. Каждый канал может одновременно наводить один истребитель на одну цель. Среднее время наведения истребителя на цель 2 минуты. Станцию можно считать “системой с отказами”, так как цель, по которой наведение не началось в момент, когда она вошла в зону действия истребителей, вообще остается не атакованной. Найти среднюю долю целей, проходящих через зону действия не обстрелянными.
16. Клиенты, обращающиеся в мастерскую бытового обслуживания, образуют простейший поток с параметром l. Каждый клиент обслуживается одним мастером в течение случайного времени, подчиняющегося показательному закону с параметром m. В случае отсутствия свободных мастеров клиент не ждет, а отказывается от обслуживания. Определить, сколько необходимо иметь мастеров, чтобы вероятность отказа клиенту в обслуживании не превосходила 0, 015, если m=l.
Решить задачу при условии, что число обслуживающих рабочих равно r (r < m).
17. Поток поступления неисправной аппаратуры в мастерскую гарантийного ремонта является простейшим с параметром l=10 ед./час. Продолжительность ремонта одной единицы является случайной величиной, имеющей показательный закон распределения с параметром m=5 ед./час. Определить среднее время, проходящее от момента поступления неисправной аппаратуры до начала ремонта, если в мастерской четверо рабочих, каждый из которых одновременно ремонтирует только один прибор.
18. В травмотологическом пункте работают два врача. С какой наибольшей интенсивностью могут поступать больные, чтобы среднее число ожидающих в очереди не превосходило трех, если на оказание помощи больному в среднем затрачивается 9 мин.?
19. В мастерскую срочного ремонта обуви, имеющую двух мастеров, обращаются в среднем 18 клиентов в час, а среднее время обслуживания одного клиента 5 мин. Какова вероятность для клиента завершить починку обуви не более чем за полчаса?
20. На коммутатор, имеющий три внешние линии связи, поступает в среднем в час 60 требований на связь. Средняя продолжительность переговоров 3 мин. Определить: а) вероятность отказа абоненту; б) среднее число занятых линий.
21. На стоянке автомобилей имеется всего 10 мест, каждое из которых отводится под один автомобиль. Автомобили прибывают на стоянку в соответствии с пуассоновским потоком при средней частоте 10 автомобилей в час. Продолжительность пребывания автомобилей на стоянке распределена показательно со средним значением, равным 10 мин. Система работает достаточно долго. Найти вероятность того, что прибывший автомобиль не найдет на стоянке свободного места.
22. Пусть в системе M|M| 2 продолжительность обслуживания одного клиента равняется 5 мин., а средняя длина интервала времени между последовательными поступлениями заявок на обслуживание составляет 8 мин. Система работает достаточно долго. Найти:
а) вероятность возникновения задержки заявки в обслуживающей системе;
б) вероятность того, что хотя бы один из обслуживающих приборов будет незагруженным;
в) вероятность того, что незагруженным окажутся оба обслуживающих приборов.
23. Клиенты прибывают к ларьку, в котором продаются прохладительные напитки, в соответствии с пуассоновским потоком при средней частоте 10 человек в час. Продолжительность обслуживания клиентов распределена показательно со средним значением 5 мин. Возле ларька имеются три места для ожидания, включая площадку для стоянки трех автомобилей. Другие подъезжающие к ларьку автомобили размещаются там, где есть свободное для стоянки место (в окрестности ларька). Система работает достаточно долго. Найти:
а) вероятность того, что прибывший к ларьку клиент имеет возможность занять очередь на площадке, отведенной для ожидания;
б) вероятность того, что прибывший клиент окажется вынужденным ждать за пределами площадки, специально отведенной для ожидания обслуживания;
в) среднюю длину интервала времени, в течении которого клиент окажется вынужденным ждать обслуживания;
г) число мест для размещения возле ларька автомобилей с учетом требования, которое заключается в том, чтобы доля среднего времени пребывания клиента в очереди составляла не менее 0, 2 общего его пребывания в системе.
24. Закусочная, расположенная около автомагистрали, имеет прилавок, возле которого может остановиться один автомобиль. По статистическим оценкам автомобили подъезжают к закусочной в соответствии с пуассоновским потоком со средней частотой 2 автомобиля за 5 мин. Подъездная дорожка к закусочной позволяет встать в очередь 10 автомобилям (очевидно, что если подъездная дорожка полностью занята очередью автомобилей, то дополнительно прибывающие к месту расположения закусочной автомобили могут расположиться для ожидания в каких-нибудь других местах). Для выполнения заказов клиентов требуется в среднем по 1, 5 мин., и продолжительности обслуживания распределены по показательному закону. Требуется вычислить:
а) вероятность того, что у закусочной не окажется ни одного автомобиля;
б) среднее число ожидающих начала обслуживания клиентов;
в) среднее время ожидания от момента прибытия клиента до начала его обслуживания;
г) вероятность того, что количество прибывших к закусочной автомобилей превысит 10.
25. Рассмотрим работу пункта по обмену валюты. Клиенты приходят в пункт в соответствии с пуассоновским потоком в среднем каждые 6 минут. Время обслуживания одного клиента подчиняется показательному распределению со средним значением, равным 6 минутам. Каждый обслуженный клиент приносит доход в два доллара США (в среднем). Пункт имеет одну кассу обслуживания и два места для ожидания. Посетители, заставшие места для ожидания занятыми, теряются для системы. Для улучшения работы пункта рассматриваются два инвестиционных проекта:
а) затратив 200 долларов, оборудовать 4 места для ожидания (добавить еще два кресла);
б) затратив 1000 долларов, увеличить число мест для ожидания до 10.
Найти среднее время, за которое окупится каждый из этих проектов, если пункт работает 8 часов в сутки.
26. Предположим, что имеются три проекта строительства морского порта: П1 – Построить два порта и в каждом порту соорудить один причал; П2 – Построить один порт с двумя причалами и П3 – Построить один порт с одним причалом, но с производительностью в два раза выше, чем в предыдущих проектах. Какому из проектов следует отдать предпочтение?
27. В системе с самообслуживанием входной поток является пуассоновским и имеет интенсивность, равная 50 клиентам в час. Продолжительность обслуживания в расчете на одного клиента распределена показательно со средним значением 5 минут. Определить: а) среднее число клиентов, находящихся в произвольно выбранный момент времени в стадии обслуживания; б) часть времени, в течение которого система простаивает.