
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Процессы гибели и размножения
|
|
Процессом гибели и размножения называется однородная марковская цепь с непрерывным временем и счетным множеством состояний X={0, 1, 2, …}, в которой за время D t из состояния i возможен лишь непосредственный переход в состояния i –1 и i +1, то есть для инфинитезимальных характеристик будут выполнены следующие условия:
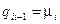 ,
, 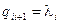 ,
, 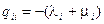 ,
,
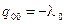 ,
, 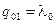 ,
,
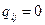 для остальных значений
для остальных значений 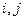 .
.
Такие процессы хорошо описывают задачи в области биологии, физики, социологии, массового обслуживания. Состояние процесса можно интерпретировать, например, как число особей некоторой популяции, переход из состояния i в i +1 – как рождение новой особи, а переход из состояния i в i –1 – как гибель некоторой особи.
Процессы гибели и размножения принято изображать в виде размеченного графа состояний, следующего вида

Рис. 6.
Вершина графа обозначает состояние цепи Маркова. Ребра графа ориентированы и показывают возможные переходы из одного состояния в другое. В графе рисуют лишь те ребра, которые показывают переходы с ненулевыми инфинитезимальными характеристиками. Эти характеристики обычно пишут рядом с ребрами и называют весами ребер. Удобство такого способа описания марковских процессов заключается в его наглядности и возможности реализации простого правила построения системы дифференциальных уравнений Колмогорова.
Правило: производная по времени от вероятности состояния в момент времени t равна сумме произведений вероятностей состояний на веса ребер, входящих в данное состояние (как будто вероятности втекают в данное состояние), минус произведение вероятности рассматриваемого состояния на сумму весов всех ребер, выходящих из него (как будто вероятность вытекает из рассматриваемого состояния).
Прямая и обратная системы дифференциальных уравнений для переходных вероятностей pij (t)процессов гибели и размножения имеют вид:
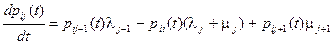 ,
,
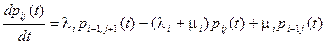 .
.
Система дифференциальных уравнений для вероятностей состояний Pi(t)=P{i(t)=i} соответственно записывается в виде:
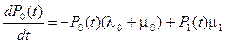 ,
,
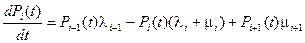 ,
, 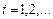
Система уравнений Колмогорова для стационарных вероятностей p j:
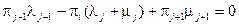
 ,
,
 ,
,
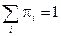 .
.
Для решения полученной системы можно применить метод Хинчина. Обозначим
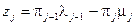 ,
,
тогда из системы уравнений следует, что
 ,
, 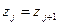 ,
, 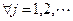
следовательно, имеет место равенство
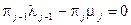 ,
,
откуда получаем равенство
 .
.
Вероятность p0 найдём из условия нормировки
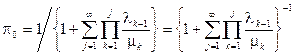 .
.
Здесь возможны два случая, связанные со сходимостью ряда:
1) 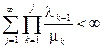 ,
,
тогда стационарные вероятности существуют и равны
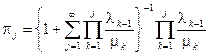 .
.
2)  ,
,
тогда не существует стационарного распределения для рассматриваемого процесса гибели и размножения.