Глава 3. Цепи Маркова с непрерывным временем

Рассмотрим марковский процесс x(t) с конечным или счетным множеством состояний X, который изменяет свои состояния в произвольные моменты времени. Такой процесс называется цепью Маркова с непрерывным временем. Очевидно, что для такой цепи Маркова выполняются условия

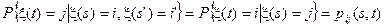
для любых i´, i, j Î X и s´ < s < t Î T.

Определение. Вероятность p_ij (s, t) называется вероятностью перехода из состояния i в состояние j за промежуток времени [ s, t).

Цепи Маркова однозначно определяются матрицей вероятностей переходов P (s, t)=|| p_ij (s, t)|| и начальным распределением q _i = P {x(0)= i }.

Вероятности состояний в любой момент времени t определяются следующим образом:

.

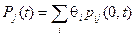Определение. Если вероятности переходов p_ij (s, t) зависят только от разности моментов времени, то есть p_ij (s, t)= p_ij (t–s)= p_ij (t), то цепь Маркова называется однородной.

Для однородных цепей Маркова матрица вероятностей переходов имеет вид P (t)=|| p_ij (t)||, а вероятности состояний определяются следующим образом:

.

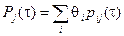Переходные вероятности обладают следующими свойствами:

.

.

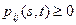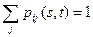Уравнение Чемпена-Колмогорова:

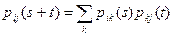– для однородных цепей Маркова,

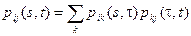– для неоднородных цепей Маркова, где s < t< t.

Условие стохастической непрерывности: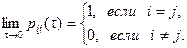

Это условие означает, что с вероятностью 1 цепь однородная Маркова не изменит своего состояния за бесконечно малый промежуток времени t®0. Следует отметить, что стохастическая непрерывность не означает непрерывность реализаций марковской цепи. Это происходит потому, что разрывы каждой реализации цепи происходят в случайные моменты времени, и вероятность того, что разрыв произойдет именно в данный момент времени i, равна нулю.

Сформулируем несколько теорем относительно вероятностей p_ij (t).

Теорема 1. Для однородной цепи Маркова вероятности p_ij (t) непрерывны по t.

Теорема 2. Для " i Î X, t > 0 вероятность p_ij (t)> 0.

Теорема 3. Если для некоторого t ₀ выполняется неравенство p_ij (t ₀)> 0, то и для всех t > t ₀ аналогично p_ij (t)> 0.

Теорема 4. Для цепи Маркова с непрерывным временем существует предел

,

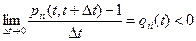хотя и может быть бесконечным.

Теорема 5. Для цепи Маркова с непрерывным временем существует и конечен предел

.

Величина q_ij (t) имеет смысл интенсивности перехода цепи Маркова из состояния i в состояние j, а величины (– q_ii (t)) – смысл интенсивности выхода из состояния i.

Кроме того, величины q_ij (t) обладают свойством

.

Из определения инфинитезимальных характеристик можно определить вероятности перехода за время D t ®0:

,

.

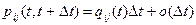Таким образом, для того чтобы задать цепь Маркова с непрерывным временем необходимо определить ее матрицу инфинитезимальных характеристик Q (t)=|| q_ij (t)||.

Матрица инфинитезимальных характеристик позволяет найти вероятности p_ij (s, t) для любых s < t. Эти вероятности удовлетворяют прямой и обратной системам дифференциальных уравнений Колмогорова.