
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
|
Задачи на составление уравнения, примеры 1-8. Содержание В14. Моторная лодка прошла 80 км от пункта А до пункта В и после трехчасовой стоянки вернулась обратно
Содержание
В14. Моторная лодка прошла 80 км от пункта А до пункта В и после трехчасовой стоянки вернулась обратно, затратив на весь путь 12 часов. Найдите скорость лодки в неподвижной воде, если скорость течения реки 2 км/ч. Ответ дайте в км/ч.
Решение:
Пусть х км/ч – скорость лодки в неподвижной воде,
тогда (х + 2) км/ч – скорость лодки по течению реки,
(х - 2)км/ч – против течения,
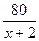 ч – время, затраченное на путь по течению, ч – время, затраченное на путь по течению,
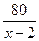 ч – против течения;
По условию задачи на весь путь затрачено 12 ч, на стоянку 3ч.
Составим уравнение: ч – против течения;
По условию задачи на весь путь затрачено 12 ч, на стоянку 3ч.
Составим уравнение: 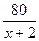 + + 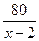 +3 = 12; +3 = 12; 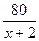 + + 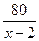 = 9.
Умножим обе части последнего уравнения на (х - 2) (х + 2), получим:
80 (х - 2) + 80 (х + 2) = 9 (х - 2) (х + 2); 80 (х - 2) + 80 (х + 2) = 9 (х ² - 4);
80 х – 160 + 80 х + 160 = 9 х ² - 36; 9 х ² - 36 - 80 х + 160 – 80 х – 160 = 0;
9 х ² - 160 х – 36 = 0; D = 160² - 4 · 9 · (-36) = 25600 + 1296 = 26896 = 164² > 0 - 2 корня;
х = = 9.
Умножим обе части последнего уравнения на (х - 2) (х + 2), получим:
80 (х - 2) + 80 (х + 2) = 9 (х - 2) (х + 2); 80 (х - 2) + 80 (х + 2) = 9 (х ² - 4);
80 х – 160 + 80 х + 160 = 9 х ² - 36; 9 х ² - 36 - 80 х + 160 – 80 х – 160 = 0;
9 х ² - 160 х – 36 = 0; D = 160² - 4 · 9 · (-36) = 25600 + 1296 = 26896 = 164² > 0 - 2 корня;
х = 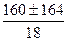 ; ; 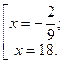 По смыслу задачи х > 2.
Значит, 18 км/ч – скорость лодки в неподвижной воде.В бланк ответов: 18 По смыслу задачи х > 2.
Значит, 18 км/ч – скорость лодки в неподвижной воде.В бланк ответов: 18
|
В13. Из пункта А в пункт В вниз по течению реки отправились одновременно моторная лодка и байдарка. Скорость течения реки равна 3 км/ч. Последнюю 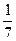 часть пути моторная лодка шла с выключенным мотором, и ее скорость относительно берега была равна скорости течения. На той части пути, где моторная лодка шла с включенным мотором, ее скорость была на 2 км/ч больше скорости байдарки. Найдите скорость байдарки в неподвижной воде, если в пункт В байдарка и моторная лодка прибыли одновременно.
Решение:
Пусть х км/ч - скорость байдарки в неподвижной воде,
тогда (х + 3) км/ч - скорость байдарки по течению реки,
(х + 3 + 2 = х + 5) км/ч - скорость лодки по течению реки,
принимая все расстояние за 1, часть пути моторная лодка шла с выключенным мотором, и ее скорость относительно берега была равна скорости течения. На той части пути, где моторная лодка шла с включенным мотором, ее скорость была на 2 км/ч больше скорости байдарки. Найдите скорость байдарки в неподвижной воде, если в пункт В байдарка и моторная лодка прибыли одновременно.
Решение:
Пусть х км/ч - скорость байдарки в неподвижной воде,
тогда (х + 3) км/ч - скорость байдарки по течению реки,
(х + 3 + 2 = х + 5) км/ч - скорость лодки по течению реки,
принимая все расстояние за 1,
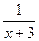 ч – время, затраченное байдаркой на весь путь, ч – время, затраченное байдаркой на весь путь,
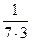 ч - время, затраченное лодкой на последнюю ч - время, затраченное лодкой на последнюю 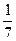 часть пути, часть пути,
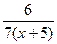 ч - время, затраченное лодкой на 1 - ч - время, затраченное лодкой на 1 - 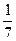 = = 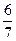 часть пути.
По условию задачи байдарка и моторная лодка прибыли одновременно, затрачивая, очевидно, одинаковое время.
Составим уравнение: часть пути.
По условию задачи байдарка и моторная лодка прибыли одновременно, затрачивая, очевидно, одинаковое время.
Составим уравнение: 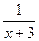 = = 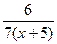 + + 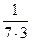 . Умножим обе части уравнения на 7·3(х + 3)(х + 5), получим: 21 х + 105 = 18 х + 54 + х ² + 8 х + 15, х ² + 5 х – 36 = 0,
D = 25 + 144 = 169 = 13² > 0 - 2 корня, х = . Умножим обе части уравнения на 7·3(х + 3)(х + 5), получим: 21 х + 105 = 18 х + 54 + х ² + 8 х + 15, х ² + 5 х – 36 = 0,
D = 25 + 144 = 169 = 13² > 0 - 2 корня, х = 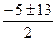 , , 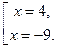 По смыслу задачи х > 3.
Значит, 4 км/ч - скорость байдарки в неподвижной воде.
В бланк ответов: 4 По смыслу задачи х > 3.
Значит, 4 км/ч - скорость байдарки в неподвижной воде.
В бланк ответов: 4
|
Пример 9.
Данная страница нарушает авторские права?