
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Логарифмическая зависимость: .
|
|
Значимость а1 и а2 определяется по той же схеме. Вместо хi и 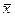 берутся
берутся 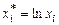 и
и 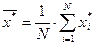 .
.
Параболическая зависимость: 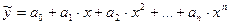
Для проверки значимости коэффициента ак (k = 1, 2..n), значение tрасч определяется по формуле:
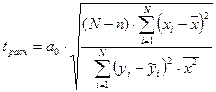
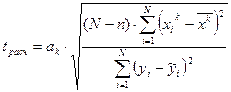 ,
,
где n – число коэффициентов регрессии.
При определении значимости коэффициента а0 в формуле tрасч показатели степени к при хi и 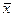 берутся равными единице (k= 1).
берутся равными единице (k= 1).
Тригонометрическая зависимость:
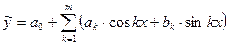
представляется в виде линейной зависимости: 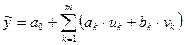 ,
,
где 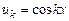 ,
, 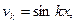
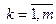 .
.
Значимость коэффициента ак, ( 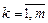 ) оценивают по формуле:
) оценивают по формуле:
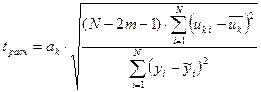 .
.
Значимость коэффициента bк ( 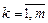 )определяют по формуле:
)определяют по формуле:
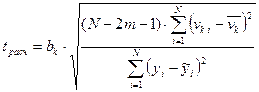 .
.
Значимость коэффициента а0 ( 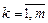 )рассчитывают по формуле:
)рассчитывают по формуле:
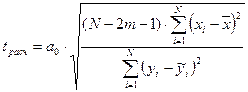
Оценка значимости коэффициента детерминации
(значимость уравнения регрессии в целом)
После оценки значимости параметров регрессии обычно анализируется совокупная значимость параметров, которая позволяет оценить уравнение регрессии в целом. Эта оценка позволяет узнать пригодно уравнение для прогноза или нет.
Для этих целей используют гипотезу о статистической значимости коэффициента детерминации
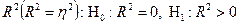
Для проверки используют F-статистику: 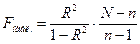 , где N – число наблюдений, n – число параметров. Величина F имеет распределение Фишера-Снедеккора. По таблице критических точек Фишера-Снедеккора. Находят
, где N – число наблюдений, n – число параметров. Величина F имеет распределение Фишера-Снедеккора. По таблице критических точек Фишера-Снедеккора. Находят 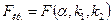 , где
, где 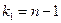 ,
, 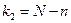 . Нулевая гипотеза отклоняется, если
. Нулевая гипотеза отклоняется, если 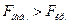 , это равносильно тому, что
, это равносильно тому, что 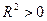 , т.е.
, т.е. 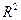 статистически значим или, что тоже самое, значимо все уравнение регрессии.
статистически значим или, что тоже самое, значимо все уравнение регрессии.
Если 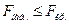 , то
, то 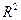 незначим, следовательно и уравнение регрессии в целом незначимо.
незначим, следовательно и уравнение регрессии в целом незначимо.
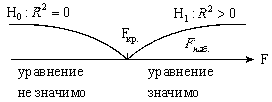
Рис. 3
Автокорреляция остатков. Критерий Дарбина – Уотсона
Статистическая значимость коэффициентов регрессии не гарантирует высокое качество уравнения регрессии. При анализе уравнения регрессии на начальном этапе часто проверяют выполнимость одной предпосылки, которую можно сформулировать как статистическая независимость отклонений (остатков ei ) между собой.
При этом проверяют некоррелированность остатков, причем не любых, а только соседних величин ei, 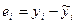 .
.
Соседними считают соседние во времени (при рассмотрении временных рядов) или по возрастанию переменной х значения ei. Для этих величин рассчитывают коэффициент корреляции reiei-1, который называется коэффициентом корреляции первого порядка:
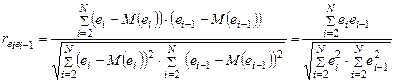 ,
,
где M(ei) = M(ei-1) = 0
Наиболее известным методом определения автокорреляции первого порядка является критерий Дарбина – Уотсона (DW).
Автокорреляция, или последовательная корреляция, определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве.
Суть метода Дарбина – Уотсона состоит в том, что на основании критерия DW Дарбина – Уотсона делается вывод об автокорреляции. На практике вместо коэффициента корреляции reiei-1 используют критерий:
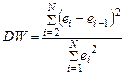
Предполагая, что 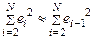 (при больших N соотношение справедливо), критерий DW можно привести к более простому виду. Действительно, тогда
(при больших N соотношение справедливо), критерий DW можно привести к более простому виду. Действительно, тогда 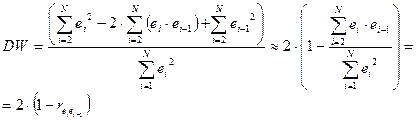 Поскольку коэффициент корреляции находится в пределах
Поскольку коэффициент корреляции находится в пределах 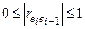 , нетрудно заметить, что:
, нетрудно заметить, что:
ü если 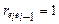 , то DW = 0 (положительная автокорреляция);
, то DW = 0 (положительная автокорреляция);
ü если 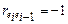 , то DW = 4 (отрицательная автокорреляция);
, то DW = 4 (отрицательная автокорреляция);
ü если 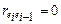 , то DW = 2 (автокорреляция отсутствует).
, то DW = 2 (автокорреляция отсутствует).
Таким образом, 0 £ DW £ 4. Для более точного определения автокорреляции была построена таблица критических точек распределения Дарбина – Уотсона. По ней для заданного уровня значимости a, числа наблюдений N и количества параметров m уравнения регрессии определяются два значения:
d1 – нижняя граница,
d2 – верхняя граница.
Фрагмент таблицы критических границ DW – критерия для a = 0.05, m = 1 приведен ниже:
Таблица 4.
| Критические границы | Число наблюдений N | ||||||
| d1 | 1, 08 | 1, 20 | 1, 35 | 1, 41 | 1, 50 | 1, 56 | 1, 65 |
| d2 | 1, 36 | 1, 41 | 1, 49 | 1, 53 | 1, 59 | 1, 63 | 1, 69 |
Общая схема метода Дарбина – Уотсона следующая:
1. По уравнению регрессии определяются остатки 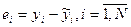 .
.
2. Рассчитывается критерий DW по формуле: 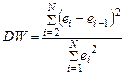 .
.
3. По таблице критических точек Дарбина – Уотсона определяют два числа d1 и d2 и осуществляют выводы по правилу, по которому рассматривают нулевую гипотезу H0 об отсутствии автокорреляции остатков. Для этого используют числовой отрезок (Рис.4.):
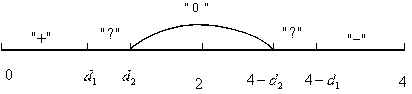
Рис.4.
1) 0 £ DW < d1 – существует положительная автокорреляция (H0отвергается), “+”;
2) d1 £ DW < d2 – вывод о наличии автокорреляции не определен, “? ”;
3) d2 £ DW < 4-d2 – автокорреляция отсутствует (H0 принимается), “0”;
4) 4-d2 £ DW < 4-d1 - вывод о наличии автокорреляции не определен, “? ”;
5) 4-d1 £ DW < 4 – существует отрицательная автокорреляция (H0отвергается), “-”.
Например, пусть N = 20, DW, рассчитанное по формуле пункта 2, равно 2, 3 (DW=2, 3).
Так как d2 £ DW < 4-d2 (1, 41 < 2.3 < 2.59), то можно считать, что автокорреляция остатков отсутствует.