Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение типовых задач
|
|
Пример 5.1. Система представляет собой техническое устройство, состоящего из m узлов (m = 3) и время от времени (в моменты 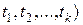 подвергается профилактическому осмотру и ремонту. После каждого шага (момент осмотра и ремонта) система может оказаться в одном из следующих состоянии:
подвергается профилактическому осмотру и ремонту. После каждого шага (момент осмотра и ремонта) система может оказаться в одном из следующих состоянии: 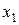 – все узлы исправны;
– все узлы исправны; 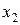 – один узел заменен новым, остальные исправны;
– один узел заменен новым, остальные исправны; 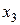 – два узла заменены новыми, остальные исправны;
– два узла заменены новыми, остальные исправны; 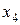 – все три узла заменены новыми. Рассматривая состояния системы как марковскую цепь, вычислить вероятности состояний после трех шагов, т.е.
– все три узла заменены новыми. Рассматривая состояния системы как марковскую цепь, вычислить вероятности состояний после трех шагов, т.е. 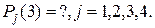 В начальный момент времени все узлы исправны. Матрица перехода
В начальный момент времени все узлы исправны. Матрица перехода 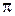 имеет вид:
имеет вид:
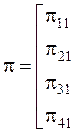
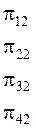

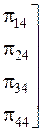
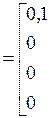
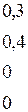
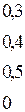
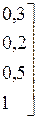
Таким образом:
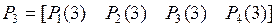 =?
=?
Решение. Определим матрицу 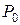 :
:
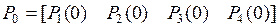
Так как в начальный момент времени система находится в состоянии 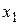 , то:
, то:
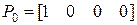
Из (5.7) имеем:
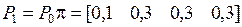
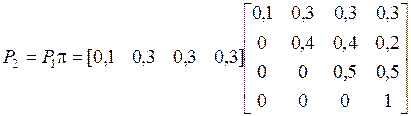 ;
;
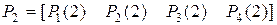 .
.
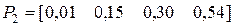 ;
;
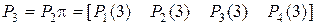
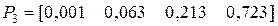
Пример 5.2. Задана матрица перехода 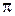 вида:
вида:

Найти матрицу финальных вероятностей Т вида:
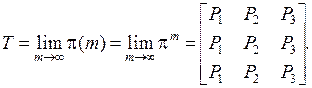
Решение. Из ( 5.9 ) имеем для n = 3:
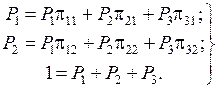
или
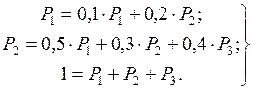 ( 5.10 )
( 5.10 )
Из ( 5.10 ) имеем:
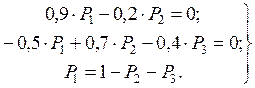 ( 5.11 )
( 5.11 )
Из ( 5.11 ) имеем:
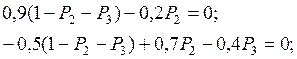
или
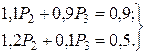 ( 5.12 )
( 5.12 )
Решим систему уравнений ( 5.12 ), используя правило Крамера. Имеем:
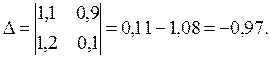
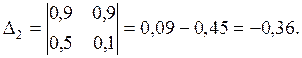
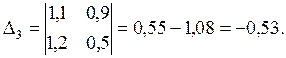
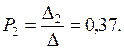
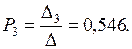
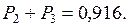
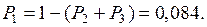
Таким образом: