Теоретические сведения. Основной задачей исследования марковской цепи является нахождение безусловных вероятностей нахождения системы S на любом (k-м) шаге в состоянии обозначим эту

Основной задачей исследования марковской цепи является нахождение безусловных вероятностей нахождения системы S на любом (k -м) шаге в состоянии 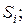обозначим эту вероятность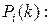

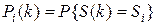
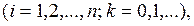( 5.1 )

где n – число дискретных состояний системы S.

Для нахождения вероятностей 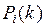необходимо знать условные вероятности перехода системы S на k -м шаге в состояние 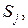если известно, что на предыдущем (k – 1)-м шаге она была в состоянии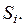

Обозначим эту вероятность:

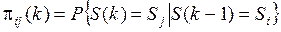
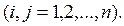( 5.2 )

Вероятности 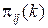называются вероятностями перехода цепи Маркова на k -м шаге.

Вероятности перехода можно записать в виде матрицы перехода 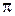размерности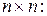

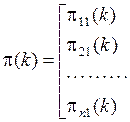
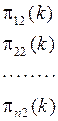
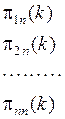
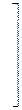
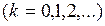( 5.3 )

Цепь Маркова называется однородной, если не зависят от номера шага 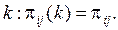Соотношение ( 5.3) примет вид:

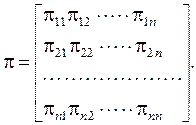( 5.4 )

Матрица безусловных вероятностей состояний на шаге k определяется соотношением:

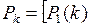
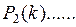
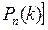
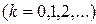( 5.5 )

Для 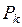справедливо соотношение:

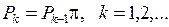( 5.6 )

Из (5. 6 ) имеем:

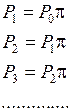( 5.7 )

Матрица финальных вероятностей Т вида:

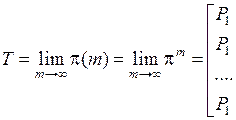
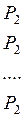
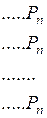
(5. 8 )

может быть определена путем решения системы алгебраических уравнений:

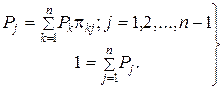( 5.9 )

Здесь 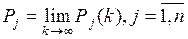– финальные вероятности.