
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение типовых задач. Пример 6.1. Определить число кладовщиков, распределяющих инструмент, оптимальное с точки зрения минимума потерь рабочего времени как у рабочих
|
|
Пример 6.1. Определить число кладовщиков, распределяющих инструмент, оптимальное с точки зрения минимума потерь рабочего времени как у рабочих, так и у кладовщиков. Данные для решения
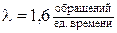 – интенсивность обращения рабочих к кладовщикам;
– интенсивность обращения рабочих к кладовщикам;
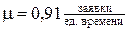 – интенсивность обслуживания заявок рабочих на инструмент одним кладовщиком;
– интенсивность обслуживания заявок рабочих на инструмент одним кладовщиком;
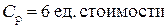 – стоимость 1 часа простоя одного рабочего;
– стоимость 1 часа простоя одного рабочего;
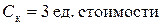 – стоимость 1 часа простоя одного кладовщика.
– стоимость 1 часа простоя одного кладовщика.
Решение. Пусть за смену за инструментом обратится N р рабочих. Если каждый из них в среднем проведет в очереди время  , то потери составят
, то потери составят
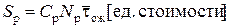 .
.
Если в течение смены каждый кладовщик будет время 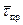 ожидать прихода рабочих, то потери составят
ожидать прихода рабочих, то потери составят
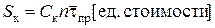 ,
,
где n – число кладовщиков.
Суммарные потери
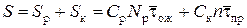 .
.
Так как 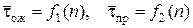 ,
,
то
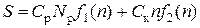
является функцией от n. Следовательно, задача сводится к определению такого значения n, при котором величина S обращается в минимум. Т.о., задача сводится к поиску зависимости 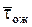 и
и 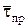 от n.
от n.
Организационно система раздачи инструмента построена таким образом, что имеется одно окно раздачи (общая очередь рабочих), которое обслуживается несколькими кладовщиками. Т.о., имеем модель многоканальной СМО с ожиданием и с одной общей очередью. Число мест в очереди неограничено.
Переходим к числовым расчетам, связанным с определением оптимального значения n. Вычислять  будем только для тех случаев, когда
будем только для тех случаев, когда 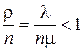 . Поэтому для n= 1 расчетов вести не следует, т.к.
. Поэтому для n= 1 расчетов вести не следует, т.к. 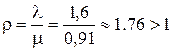 , а это значит, что один кладовщик не справляется с очередью и очередь увеличивается непрерывно в течение всей смены.
, а это значит, что один кладовщик не справляется с очередью и очередь увеличивается непрерывно в течение всей смены.
Определим по формулам (6.14), (6.16), (6.17)  и
и 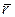 для различных значений n. Для n = 2 имеем
для различных значений n. Для n = 2 имеем
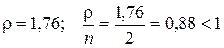
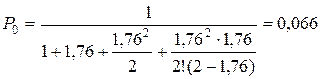
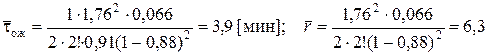 .
.
Для n = 3 имеем
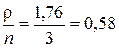 ;
;
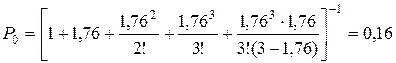 ;
;
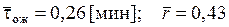 .
.
Для n = 4 получим
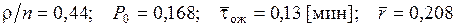 .
.
Если принять за единицу времени минуту, то в течение 8-часового рабочего дня на пункт раздачи инструмента придет число рабочих
 .
.
Т.о. число заявок в течение рабочего дня равно 768. Один кладовщик затрачивает на выполнение одной заявки в среднем время, равное 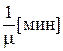 . Тогда общее время занятости кладовщиков равно
. Тогда общее время занятости кладовщиков равно
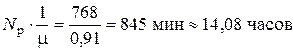
Ежедневная продолжительность простоя кладовщиков определяется по формуле
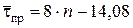
для n = 2
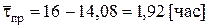
для n = 3
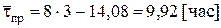
для n = 4
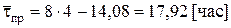
Для каждого из этих случаев вычислим время, потерянное рабочими из-за ожидания в очереди. Имеем
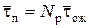 .
.
Для n = 2 имеем
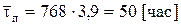
Для n = 3 получим
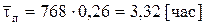
Для n = 4 имеем
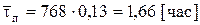
Общая ежедневная стоимость времени, потерянного рабочими и кладовщиками
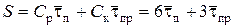 .
.
Для n = 2 имеем
 .
.
Для n = 3 получим
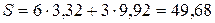 .
.
Для n = 4 имеем
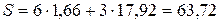 .
.
Следовательно, S достигает минимума при n = 3.
Таким образом, три кладовщика в данных условиях обеспечивают минимум потерь, связанных со случайным характером обслуживания рабочих.