
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические сведения. Система массового обслуживания (СМО) называется системой с ожиданием, если заявка, заставшая все каналы обслуживания занятыми
|
|
Система массового обслуживания (СМО) называется системой с ожиданием, если заявка, заставшая все каналы обслуживания занятыми, становится в очередь и ждет, пока не освободится какой-нибудь канал.
Рассмотрим n -канальную СМО. Поток заявок пуассоновский с интенсивностью 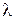 .
. 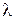 представляет собой среднее число заявок, приходящихся на единицу времени. Поток обслуживания заявок одним каналом пуассоновский с интенсивностью
представляет собой среднее число заявок, приходящихся на единицу времени. Поток обслуживания заявок одним каналом пуассоновский с интенсивностью 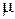 .
. 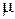 представляет собой среднее число обслуженных заявок, приходящееся на единицу времени. 2 занятых канала имеют интенсивность обслуживания заявок, равную 2
представляет собой среднее число обслуженных заявок, приходящееся на единицу времени. 2 занятых канала имеют интенсивность обслуживания заявок, равную 2 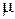 . k занятых каналов имеют интенсивность обслуживания заявок, равную k
. k занятых каналов имеют интенсивность обслуживания заявок, равную k 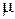 . Число мест в очереди неограниченно.
. Число мест в очереди неограниченно.
Составим перечень состояний системы. Имеем:
x 0 – все каналы свободны
x 1 – занят 1 канал, остальные свободны
x 2 – занято 2 канала, остальные свободны
xk – занято k каналов, остальные свободны
xn – заняты все n каналов
xn+ 1 – заняты все n каналов, одна заявка стоит в очереди
xn+ 2 – заняты все n каналов, две заявки стоят в очереди
xn+r – заняты все n каналов, r заявок стоят в очереди
Приведем граф состояния СМО. Имеем

Рис. 6.1
Обозначим через Pk (t)(k = 0, 1, …, n+r, …) вероятности состояний системы в момент времени t. Правило составления дифференциальных уравнений для вероятностей P 0(t), P 1(t), …, Pn+r (t), … следующее:
1) Производная вероятности данного состояния равно определенной сумме слагаемых.
2) Число слагаемых равно числу стрелок, соединяющих данное состояние со всеми остальными состояниями.
3) Слагаемое берется со знаком “+”, если стрелка направлена к данному состоянию и со знаком “–”, если стрелка направлена от данного состояния.
4) Каждое слагаемое равно произведению вероятности того состояния, из которого выходит стрелка, на интенсивность пуассоновского потока по этой стрелке.
Пользуясь правилом построения дифференциальных уравнений на основе графа состояний, получим систему дифференциальных уравнений для вероятностей состояний вида

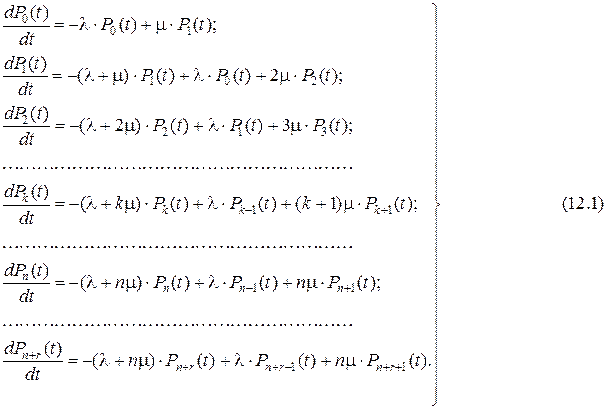 Так как СМО может находиться только в одном из состояний, то справедливо соотношение
Так как СМО может находиться только в одном из состояний, то справедливо соотношение
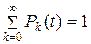 . (6.2)
. (6.2)
В установившемся режиме имеем
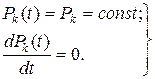 (6.3)
(6.3)
В результате получим из (6.1) систему алгебраических уравнений вида
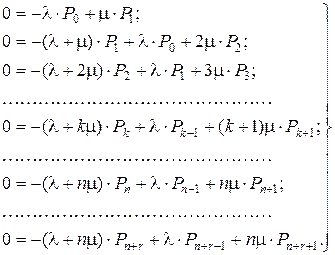 (6.4)
(6.4)
Из 1-го уравнения системы (6.4) имеем
 , (6.5)
, (6.5)
где
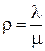 . (6.6)
. (6.6)
Из 2-го уравнения системы (6.4) получим
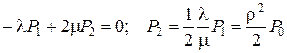 .
.
Из 3-го уравнения системы (6.4) имеем
 .
.
Для любого k < n получим
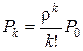 . (6.7)
. (6.7)
Для k = n имеем
 . (6.8)
. (6.8)
Для k = n+1 имеем
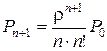 .
.
Для k = n+2 имеем
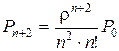 .
.
Для k = n+r имеем
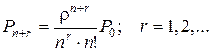 . (6.9)
. (6.9)
Из уравнения

имеем
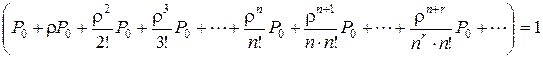
Откуда
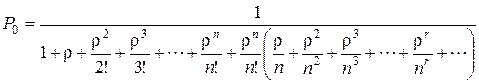 . (6.10)
. (6.10)
Имеем
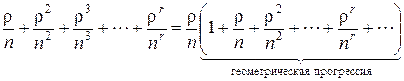 . 6.11)
. 6.11)
Введем обозначение
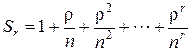 . (6.12)
. (6.12)
Пусть
 .
.
Тогда
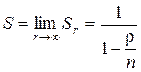 . (6.13)
. (6.13)
Соотношение (6.10) с учетом (6.11) – (6.13) примет вид
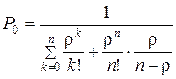 . (6.14)
. (6.14)
Определим среднее число заявок в очереди, умножая возможное число заявок в очереди на вероятность того, что именно это число заявок будет в очереди, и складывая результаты
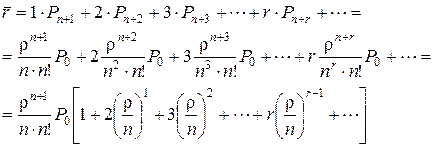
Учтем следующее равенство
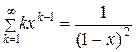 . (6.15)
. (6.15)
Следовательно
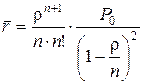 . (6.16)
. (6.16)
Определим среднее время ожидания заявки в очереди 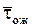 до выполнения заявки СМО. Если заявка застанет не все каналы занятыми, то ей не придется ждать. Если заявка придет в момент, когда заняты все n каналов, но очереди нет, то она будет ждать обслуживания в среднем время, равное
до выполнения заявки СМО. Если заявка застанет не все каналы занятыми, то ей не придется ждать. Если заявка придет в момент, когда заняты все n каналов, но очереди нет, то она будет ждать обслуживания в среднем время, равное 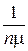 , где n μ – среднее число заявок, обслуженное СМО в единицу времени;
, где n μ – среднее число заявок, обслуженное СМО в единицу времени; 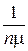 – среднее время обслуживания одной заявки. Если заявка застанет одну заявку в очереди, то ей придется ждать в очереди время, равное
– среднее время обслуживания одной заявки. Если заявка застанет одну заявку в очереди, то ей придется ждать в очереди время, равное 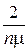 . Если заявка застанет в очереди r заявок, то ей придется ждать в очереди время
. Если заявка застанет в очереди r заявок, то ей придется ждать в очереди время 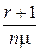 . Следовательно
. Следовательно
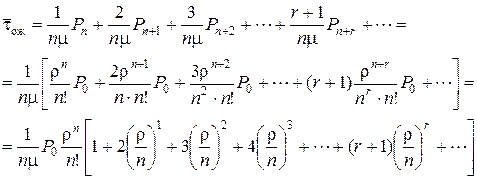
Полученное соотношение с учетом (6.15) примет вид
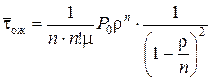 . (6.17)
. (6.17)
Среднее число простаивающих каналов обслуживания заявок определяется формулой
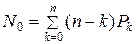 . (6.18)
. (6.18)
Среднее время обслуживания
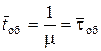 , (6.19)
, (6.19)
т.е. совпадает со средней длительностью обслуживания заявки.
Среднее время пребывания заявки в СМО с ожидание
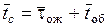 . (6.20)
. (6.20)
Среднее число занятых каналов  равно
равно
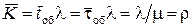 . (6.21)
. (6.21)
Значение критерия эффективности
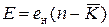 , (6.22)
, (6.22)
где e н – штраф за неиспользование одного канала обслуживания.
Загрузка СМО
 . (6.23)
. (6.23)
Среднее число заявок в СМО
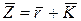 . (6.24)
. (6.24)
Рассмотрим еще один класс СМО – СМО замкнутого типа. Для замкнутых СМО характерно конечное число заявок, циркулирующих в системе “источник заявок – СМО”. Параметры суммарного входного потока заявок СМО зависят от состояния самой СМО.
Примером замкнутой СМО может служить вычислительная система оперативной обработки с диалоговым режимом работы. Система оперативной обработки содержит М терминалов Т 1 -ТМ, за каждым из которых работает пользователь П, формирующий запросы на обслуживание заявки (рис. 6.2).
Обслуживание запросов выполняется совокупностью из n однотипных ЭВМ (n ≤ М), рассматриваемых без детализации внутренней структуры как каналы с длительностью обслуживания, распределенной по экспоненциальному закону с математическим ожиданием 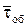 . Все ресурсы некоторой ЭВМ (канала обслуживания) полностью монополизируется назначенной на обслуживание заявкой до конца ее обслуживания. Заявка, заставшая все каналы занятыми, занимает место в очереди, число мест в которой r = M – n; заявки считаются терпеливыми, т.е. попав в СМО, непременно дождутся конца обслуживания.
. Все ресурсы некоторой ЭВМ (канала обслуживания) полностью монополизируется назначенной на обслуживание заявкой до конца ее обслуживания. Заявка, заставшая все каналы занятыми, занимает место в очереди, число мест в которой r = M – n; заявки считаются терпеливыми, т.е. попав в СМО, непременно дождутся конца обслуживания.
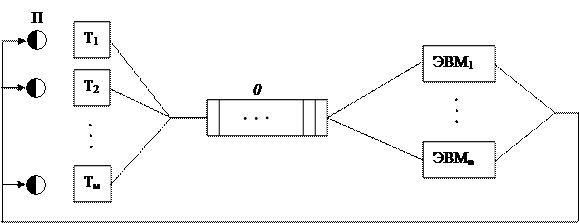
Рис. 6.2
Формирование нового запроса пользователь начинает лишь после получения ответа на предыдущий запрос, причем время, необходимое пользователю для формирования очередного запроса, будем считать распределенным экспоненциально с математическим ожиданием 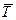 , что позволяет рассматривать пользователя как источник пуассоновского потока заявок с интенсивностью
, что позволяет рассматривать пользователя как источник пуассоновского потока заявок с интенсивностью 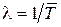 .
.
Построим граф состояний такой СМО (рис. 6.3).
 Рис. 6.3
Рис. 6.3
Возможные состояния системы будем связывать с числом пользователей, ожидающих ответа на сделанные запросы, т.е. с числом заявок, находящихся на обслуживании и в очереди: x 0 – в системе нет ни одной заявки, ЭВМ простаивают, все пользователи независимо друг от друга заняты подготовкой запросов; следовательно, интенсивность суммарного потока заявок, переводящего СМО в состояние x 1, равна M λ; x 1 – в системе одна заявка, обслуживанием которой занята одна ЭВМ, пославший запрос пользователь ждет ответа на свой запрос и не формирует новых запросов; следовательно, интенсивность потока перехода в состояние x 2 равна (M- 1)λ; интенсивность потока переходов в состояние x 0 связана с интенсивностью суммарного потока обслуживаний, равной произведению числа занятых ЭВМ на интенсивность потока обслуживаний одной ЭВМ, т.е. 1μ, …; xn – в системе n заявок, все ЭВМ заняты обслуживанием запросов пользователей, очереди на обслуживание еще нет, интенсивность суммарного потока заявок равна (M-n)λ, суммарного потока обслуживаний – n μ; xn+ 1 – в системе n+ 1 заявка, все ЭВМ заняты, одна заявка стоит в очереди на обслуживание, интенсивность суммарного потока заявок равна [ M- (n+ 1)]λ = [ M- (n+r)] λ, где r= 1 – длина очереди, суммарный поток обслуживаний имеет интенсивность n μ; xn+r – в системе n+r=M заявок, т.е. все пользователи сформировали и ввели в систему запросы на обслуживание, n ЭВМ обслуживает n заявок, r=M-n заявок находится в очереди на обслуживание, интенсивность суммарного потока заявок равна нулю, так как все пользователи ждут ответа на свои запросы, интенсивность суммарного потока обслуживания равна n μ.
Предельные вероятности состояний:
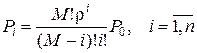 ; (6.25)
; (6.25)
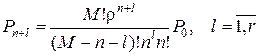 ; (6.26)
; (6.26)
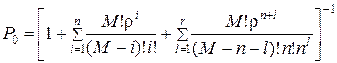 . (6.27)
. (6.27)
Среднее число занятых каналов обслуживания 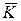 можно найти как математическое ожидание числа занятых каналов:
можно найти как математическое ожидание числа занятых каналов:
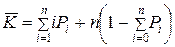 . (6.28)
. (6.28)
Среднее время ожидания заявки в очереди
 . (6.29)
. (6.29)
Среднее время пребывания заявки в системе
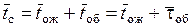 , (6.30)
, (6.30)
где 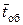 – среднее время обслуживания;
– среднее время обслуживания; 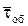 – средняя длительность обслуживания заявки.
– средняя длительность обслуживания заявки.
Среднее число заявок, связанных с системой
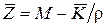 . (6.31)
. (6.31)
Зная 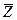 и
и  , найдем среднюю длину очереди
, найдем среднюю длину очереди
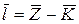 . (6.32)
. (6.32)
Загрузка системы
 . (6.33)
. (6.33)
Значение критерия эффективности
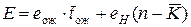 , (6.34)
, (6.34)
где  – штраф за ожидание заявки в очереди.
– штраф за ожидание заявки в очереди.