
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Править] История
|
|
Формула Эйлера
ln(cos x + i sin x)=ix
У этого термина существуют и другие значения, см. Список объектов, названных в честь Леонарда Эйлера#Формулы.
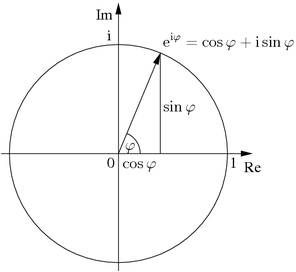

Геометрический смысл формулы Эйлера
Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями.
Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство:
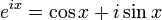 ,
,
где e — основание натурального логарифма,
i — мнимая единица.
| Содержание [убрать] · 1 История · 2 Производные формулы · 3 Применение в комплексном анализе · 4 Взаимосвязь с тригонометрией · 5 Доказательство · 6 Показательная форма комплексного числа · 7 См. также · 8 Литература |
править] История
Формула Эйлера впервые была приведена в книге «Гармония мер» английского математика Роджера Котса (помощника Ньютона), которая была издана в 1722 году, уже после смерти автора. Котс открыл формулу около 1714 года и выразил её в логарифмической форме:
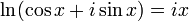 .
.
Эйлер опубликовал формулу в её привычном виде в статье 1740 года и в книге «Введение в анализ бесконечно малых» (1748), построив доказательство на равенстве бесконечных разложений в степенные ряды правой и левой частей. Ни Эйлер, ни Котс не представляли себе геометрической интерпретации формулы: представление о комплексных числах как точках на комплексной плоскости появилось примерно 50 лет спустя (см. Г. Вессель).