Edit] Using calculus

Another proof ^[7] is based on the fact that all complex numbers can be expressed in polar coordinates. Therefore for some r and θ depending on x,

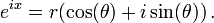Now from any of the definitions of the exponential function it can be shown that the derivative of e^ix is ie^ix. Therefore differentiating both sides gives

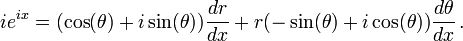
Substituting r (cos(θ) + i sin(θ)) for e^ix and equating real and imaginary parts in this formula gives 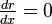and 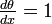. Together with the initial values r (0) = 1 and θ (0) = 0 which come from e^{i 0} = 1 this gives r = 1 and θ = x. This proves the formula e^ix = 1(cos(x) + i sin(x)).

Edit] See also

· Euler's identity

· Complex number

· Integration using Euler's formula

· List of topics named after Leonhard Euler

Edit] References

Moskowitz, Martin A. (2002). A Course in Complex Analysis in One Variable. World Scientific Publishing Co.. pp. 7. ISBN 981-02-4780-X.

2. ^ Feynman, Richard P. (1977). The Feynman Lectures on Physics, vol. I. Addison-Wesley. pp. 22-1, 22-10. ISBN0-201-02010-6.

Johann Bernoulli, Solution d'un problè me concernant le calcul inté gral, avec quelques abré gé s par rapport à ce calcul, Mé moires de l'Acadé mie Royale des Sciences de Paris, 197-289 (1702).

4. ^ John Stillwell (2002). Mathematics and Its History. Springer. https://books.google.com/books? id=V7mxZqjs5yUC& pg=PA315.

5. ^A Modern Introduction to Differential Equations, by Henry J. Ricardo, p428

6. ^ ^ab Ordinary differential equations, by Vladimir Igorevich Arnolʹ d, p166

7. ^ Strang, Gilbert (1991). Calculus. Wellesley-Cambridge. p. 389. ISBN0-9614088-2-0. https://ocw.mit.edu/resources/res-18-001-calculus-online-textbook-spring-2005/textbook/. (Second proof on page)