
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Править] Доказательство
|
|
Доказательство формулы Эйлера достаточно тривиально. Разложим функцию eix в ряд Тейлора по степеням x. Получим:
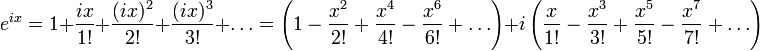
Но
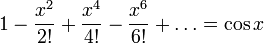

Поэтому 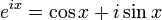
Ч. т. д.
Править] Показательная форма комплексного числа
Показательная и тригонометрические формы комплексных чисел связаны между собой формулой Эйлера.
Пусть комплексное число z в тригонометрической форме имеет вид z = r (cos φ + i sin φ). На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим:
z = rei φ
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь r = | z |, φ = argz.
Править] См. также
· Формула Муавра
· Список объектов, названных в честь Леонарда Эйлера
Править] Литература
· John Stillwell (2002). Mathematics and Its History. Springer.