Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Euler's formula
|
|
From Wikipedia, the free encyclopedia
Jump to: navigation, search
This article is about Euler's formula in complex analysis. For Euler's formula in algebraic topology and polyhedral combinatorics
see Euler characteristic.
|
Euler's formula, named after Leonhard Euler, is a mathematicalformula in complex analysis that establishes the deep relationship between the trigonometric functions and the complexexponential function. Euler's formula states that, for any real number x,
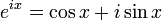
where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively, with the argument x given in radians. This complex exponential function is sometimes denoted cis (x). The formula is still valid if x is a complex number, and so some authors refer to the more general complex version as Euler's formula. [1]
Richard Feynman called Euler's formula " our jewel" and " one of the most remarkable, almost astounding, formulas in all of mathematics." [2]
| Contents · 1 History · 2 Applications in complex number theory · 3 Relationship to trigonometry · 4 Other applications · 5 Definitions of complex exponentiation o 5.1 Power series definition o 5.2 Limit definition · 6 Proofs o 6.1 Using power series o 6.2 Using the limit definition o 6.3 Using calculus · 7 See also · 8 References · 9 External links |