
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Edit] Using the limit definition
|
|
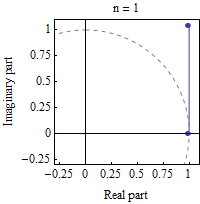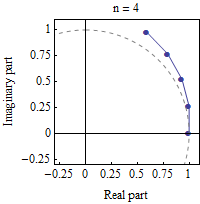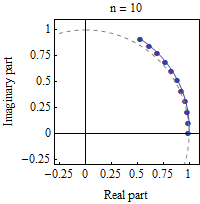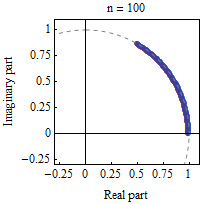

The exponential function ez can be defined as the limit of (1 + z / n) n, as n approaches infinity. In this animation, z = iπ /3, and n takes various increasing values from 1 to 100. The computation of (1 + z / n) n is displayed as the combined effect of n repeated multiplications in the complex plane. As n gets larger, the points approach the complex unit circle (dashed line), covering an angle of π /3 radians.
An alternative proof [6] starts from the limit definition of ez:
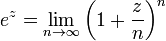 .
.
Plug in z = ix, and let n be a very large integer. Then consider the sequence:
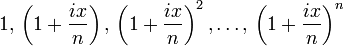
(The last element of the sequence approaches eix.) If the points of this sequence are plotted in the complex plane (see animation at right), they roughly trace out the unit circle, with each point being x / n radians counterclockwise of the previous point. (This statement is more and more and more accurate as n increases. The proof is based on the rules of trigonometry and complex-number algebra. [6] ) Therefore, in the limit the last point in the sequence, (1 + ix / n) n, is the point on the unit circle of the complex plane located x radians counterclockwise from +1, i.e. the point cos x + i sin x. Therefore, eix = cos x + i sin x.