Править] Взаимосвязь с тригонометрией

Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:

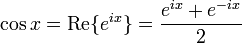
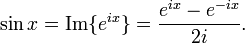
Вышеуказанные уравнения могут быть получены путем сложения или вычитания формул Эйлера:

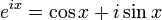
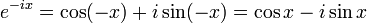
с последующим решением относительно синуса или косинуса.

Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:

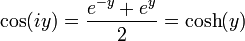
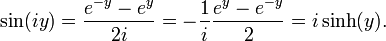
Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения, результат выражения остается вещественным. Например:

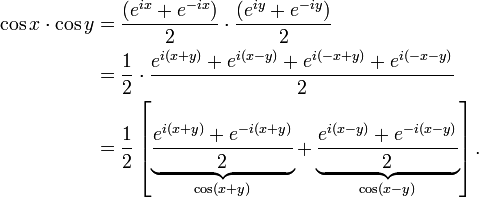
Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением. Например:

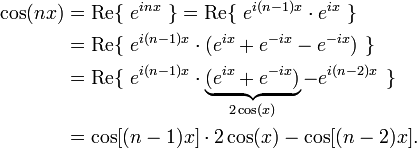
Данная формула используется для рекурсивного вычисления значений cos(nx) для целых значений n и произвольных значений x (в радианах).