Доказательство теоремы о циркуляции.

Магнитное поле может быть охарактери­зовано некоторым общим соотношением, которое, как и теорема Га­усса в электростатике, может быть использовано для расчета маг­нитных полей, создаваемых симметричными распределениями то­ков. Это соотношение носит название теоремы о циркуляции вектора магнитной индукции.

Рассмотрим произвольный замкнутый контур l и зададим на нем направление обхода. Обозначим через В_l проекцию вектора 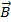на на­правление элемента контура Δ l. Составим сумму произведений В_lΔ l для всех элементов замкнутого контура. Эта сумма называ­ется циркуляцией вектора 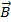по замкнутому контуру l. Можно пока­зать что, в силу закона Био-Савара – Лапласа циркуляция вектора 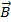по произвольному замкнутому контуру равна произведению μ _о на ток I, пронизы­вающий контур, по которому берется цир­куляция.

Проверим справедливость этого утвер­ждения для магнитного поля, создаваемого прямолинейным проводником с током. Прежде всего, отметим, что нужно рассмат­ривать только контуры, лежащие в плоско­сти, перпендикулярной проводнику, так как вектор 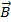в силу (4) не имеет составля­ющих, параллельных проводнику с током, и, следовательно, циркуляция 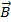по произ­вольному контуру совпадает с циркуляцией по проекции контура на эту плоскость. Проще всего рассчитать цир­куляцию 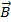по круговому контуру с центром на проводнике. В этом случае вектор 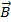в каждой точке контура параллелен элементу Δ l (ес­ли выбранное направление обхода совпадает с направлением силовых линий), а модуль В, одинаковый во всех точках контура, дается фор­мулой (6). Суммируя В_lΔ l по всем элементам контура, получаем

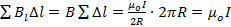. (7)

Видно, что циркуляция 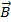не зависит от радиуса окружности. Не­трудно убедиться в том, что при произвольной деформации ок­ружности циркуляция 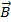не изменится. Рассмотрим элемент Δ l произвольного контура l (рис.94). Для нег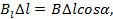о но 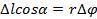, поэтому

.

Суммируя по всем элементам контура, получаем^

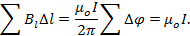
Теорема о циркуляции. Циркуляция вектора по произвольному контуру равна произведению μ _о на ток I, пронизывающий контур, по которому берется циркуляция.

Теорема о циркуляции вектора индукции магнитного поля спра­ведлива для поля, создаваемого произвольным распределением токов.

В магнитостатике теорема о циркуляции играет ту же роль, что и теорема Гаусса в электростатике. Обе теоремы являются уравнениями Максвелла, записанными в несколько другой форме, чем обычно. Уравнения Максвелла (их всего четыре) позволяют описать все явления электромагнитной теории от взаимодействия заряженных тел и токов до излучения электромагнитных волн.