Поле соленоида.

Применим теорему о циркуляции вектора ин­дукции магнитного поля к расчету поля, создава­емого соленоидом, т. е. цилиндрической катушкой с плотно соприкасающимися витками. Магнитное поле такой катушки имеет вид, показан­ный на рис. 95. Если длина ка­тушки много больше ее диамет­ра, то линии магнитной индук­ции внутри катушки парал­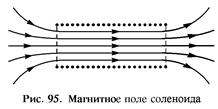 лельны ее оси и поле там одно­родно всюду, за исключением концов катушки. Снаружи вблизи бо­ковой поверхности катушки поле практически отсутствует.

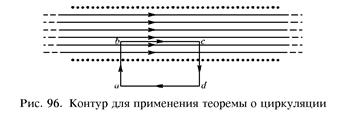
Вычислим циркуляцию индукции 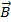по прямоугольному контуру, показанному на рис. 96: сторона bс параллельна, а стороны аb и сd перпендикулярны линиям индукции внутри катушки. Тогда вектор 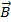будет иметь отличную от нуля проекцию на направление контура только на участке bс и циркуляция 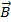по контуру равна Bl, где l – длина участка bс. Подсчитаем теперь полный ток, пронизывающий выбранный контур. Обозначим число витков на единицу длины соле­ноида через n. Сквозь выбранный контур проходит пl витков, и пол­ный ток равен Inl. Согласно теореме о циркуляции

Bl = μ _oInl,

откудa

B = μ _oIn

Эта формула дает значение индукции магнитного поля внутри длинного соленоида, по обмотке которого пропускается ток I.

Вблизи краев соленоида поле уже не будет однородным. Легко показать, что индукция поля на оси соленоида на самом его конце равна половине значения индукции внутри соленоида. Если к концу соленоида приставить другой такой же соленоид, по которому в том же направлении протекает такой же ток, то рассматриваемая точка окажется внутри нового, составного соленоида и индукция поля в ней будет определяться выведенной формулой. Но по принципу суперпози­ции эта же индукция есть сумма индукций полей, существующих вблизи концов каждого соленоида. Поскольку соленоиды одинаковы, то одинаковы и создаваемые ими поля, и, следовательно, индукция магнитного поля в точке на оси на конце одного соленоида равна В= ½ μ _o1п.